3. Расчет интерференционной картины от двух когерентных источников. Когерентность. Пространственная и временная когерентность. Оптическая разность хода волн отраженных гранями диэлектрической пленки
2) Интерференция света. Длина и время когерентности. Оптическая длина пути и оптическая разность хода лучей. Способы получения интерференционных картин.
Явление, при котором происходит пространственное перераспределение энергии светового излучения при наложении двух или нескольких световых волн, называется интерференцией.
Два колебательных процесса называются когерентными, если разность фаз Δφ=φ1 - φ2 складывающихся колебаний остается постоянной в течение времени, достаточного для наблюдений.
Свет состоит из последовательности кратковременных импульсов (цугов волн) со средней длительностью τ, фаза которых имеет случайную величину. Пусть средняя длина цугов равна l0, очевидно, что взаимодействовать между собой могут только те цуги волн, пространственное расстояние между которыми l ког < l0, в противном случае в точке наблюдения цуги, между которыми рассматривается взаимодействие, просто не встретятся. Величина l ког=l0 называется длиной когерентности, и она определяет максимально допустимую разность хода между взаимодействующими волнами, при которой еще может наблюдаться явление интерференции. А время, равное средней длительности излучения цугов, называется временем когерентности t ког=< τ >. В течение этого времени начальная фаза волны сохраняет свою постоянную величину. Время и длина когерентности связаны между собой очевидным соотношением
l ког = с*t ког
Оптическая длина пути.
L = S*n, S - геометрическая длина пути, n – показатель преломления среды.
Оптическая разность хода – разность оптических длин, проходимых волнами.
Δ = L2 - L1 = S2*n2 – S1*n1
Способы получения интерференционных картин.
Метод Юнга.Свет от ярко освещено щели падает на две щели играющие роль когерентных источников.
Зеркала Френеля.Свет от источника падает расходящимся пучком на 2 плоских зеркала, расположенных под малым углом. Роль когерентных источников играют мнимые изображения источника. Экран защищен от прямого попадания лучей заслонкой.
Бипризма Френеля. Свет от источника преломляется в призмах, в результате чего за бипризмой распространяются световые лучи, как бы исходящие из мнимых когерентных источников.
Зеркало Ллойда. Точечный источник находится близко к поверхности плоского зеркала. Когерентными источниками служат сам источник и его мнимое изображение.
3) Волновые свойства частиц. Соотношение неопределенности Гейзенберга. Уравнение Шредингера.
Для описания квантовых систем вводится волновая функция ψ(x,y,z,t). Она определяется таким образом, что вероятность dw того что частица находится в элементе объема dV была равна: dw = | ψ^2|dV.Физический смысл имеет не сама функция, а квадрат ее модуля которым задается интенсивность волн Де Бройля.
Волновая функция, характеризующая вероятность обнаружения действия микрочастицы в элементе объема должна быть: 1) конечной; 2) однозначной; 3) непрерывной. Волновая функция удовлетворяет свойству суперпозиции.
Для описания микрочастиц используются то волновые, то корпускулярные представления. Поэтому им нельзя приписывать все свойства частиц и волн. Согласно соотношению неопределенностей Гейзенберга микрочастица е может иметь одновременно и определенную координату (x,y,z) и определенную соответствующую проекцию импульса (px,py,pz), причем неопределенности этих величин удовлетворяют условиям, т.е. произведение координаты и соответствующей ей проекции импульса не может быть меньше величины порядка h. Из соотношения следует, что, например, если частица находится в состоянии с точным значением координаты, то в этом состоянии проекция ее импульса оказывается совершенно неопределенной, и наоборот.
i*ћ* ∂ψ/ ∂t = - ћ^2 *Δψ/ 2m + U(x,y,z,t)* ψ
m – масса микрочастицы, Δ - оператор Лапласа (в декартовых координатах оператор Лапласа имеет вид Δ= ∂^2/∂x^2 + ∂^2/∂y^2 + ∂^2/∂z^2), U(x,y,z,t) − функция координат и времени, описывающая воздействие на частицу силовых полей.
Уравнение называется общим уравнением Шредингера. Оно дополняется условиями, накладываемыми на функцию Ψ :
1) Ψ − конечная, непрерывная и однозначная.
2) производные от Ψ по x, y, z, t непрерывны.
3) функция |Ψ|^2 должна быть интегрируема.
ћ^2 *Δψ/ 2m + (E - U(x,y,z,t))* ψ = 0
Это уравнение не содержит времени и называется стационарным уравнением Шредингера.
.
Билет №10
2)Явление, при котором происходит пространственное пере-распределение энергии светового излучения при наложении двух или нескольких световых волн, называется интерференцией.
Интерференция - одно из явлений, в котором проявляются волновые свойства света. Необходимым условием интерференции волн является их когерентность.
Два колебательных процесса называются когерентными, ес-ли разность фаз складывающихся колебаний остается постоянной в течение времени, достаточного для наблюдений.
Одним из способов получения гогерентных волн является деление волны по фронту, но
две и более когерентные волны можно также получить путем деления исходной волны по амплитуде.
Именно таким образом когерентные волны получаются при наблюдении явлений интерференции света в тонких пленках.
Полосы равной толщины возникают при отражении парал-лельного пучка лучей от поверхности тонкой пленки, толщина которой неодинакова и меняется по какому-либо закону. Оптическая разность хода интерферирующих лучей будет меняться при переходе от одних точек поверхности пленки к другим из-за изменения толщины пленки. Интенсивность света будет одинакова в тех точках, где одинакова толщина пленки, поэтому интерференционная картина называется полосами равной толщины. Полосы равной толщины локализованы вблизи поверхности пленки.
Пусть на плоскопараллельную пластину толщиной h и с показателем преломления n падает рассеянный монохроматический свет с длиной волны λ. Из условия Δ = 2nh cosβ следует, что при n,h = const разность хода зависит только от угла падения лучей β. Очевидно, что лучи, падающие под одним углом, будут иметь одну и ту же разность хода. Если параллельно пластине разместить линзу L, в фокальной плоскости которой расположен экран Э, то эти лучи соберутся в одной точке экрана
В рассеянном свете имеются лучи самых разных направлений. Лучи, падающие на пластину под углом α1, соберутся на экране в точке Р1, интенсивность света в которой определяется разностью хода Δ. Таким образом, лучи, падающие на пластину во всевозможных плоскостях, но под углом α1, создают на экране совокупность одинаково освещенных точек, расположенных на окружности с центром в точке О. Аналогично, лучи, падающие под другим углом α2, создадут на экране совокупность одинаково освещенных точек, но расположенных на окружности другого радиуса. Следовательно, на экране будет наблюдаться система концентрических окружностей, называемых линиями равного наклона.
Классическим примером полос равной толщины являются кольца Ньютона. Ньютон наблюдал интерференционные полосы воздушной прослойке между плоской поверхностью стекла и плосковыпуклой линзой с большим радиусом кривизны, прижат стеклу. При нормальном падении света на линзу интерференционные полосы имеют форму концентрических колец, при наклонном - эллипсов. Они получаются вследствие интерференции лучей, отраженных от верхней и нижней границ воздушной прослойки между линзой и стеклянной пластиной.
3) Ядерными реакциями называются превращения атомных ядер, вызванные их взаимодействием с различными частицами или друг с другом. Как правило, взаимодействие реагирующих частиц или ядер возникает благодаря действию ядерных сил при сближении частиц до расстояний ∼10-15 м.
К ядерным реакциям относятся реакции деления, синтеза, взаимодействия ядер с легкими частицами и др. При протекании любой ядерной реакции выполняются все фундаментальные законы сохранения (энергии, импульса, заряда и др.), кроме того выполняется ряд законов сохранения, специфических только для ядерных реакций, к ним относятся законы сохранения барионного (числа нуклонов) и лептонного (числа лептонов Лептонами называют класс элементарных частиц, не участвующих в сильных взаимодействиях, например электрон) зарядов.
Ядерные реакции могут сопровождаться как поглощением, так и выделением энергии. ЭнергияQ, выделяющаяся в результате реакции, определяется разностью масс покоя исходных Мi и конечных Мk ядер и частиц:
Билет №11
studfiles.net
Получение когерентных источников. Оптическая разность хода.
Все естественные источники света не когерентны. Это обусловлено тем, что излучение светящегося тела слагается из волн, испускаемых многими атомами. Отдельные атомы испускают цуги волн за 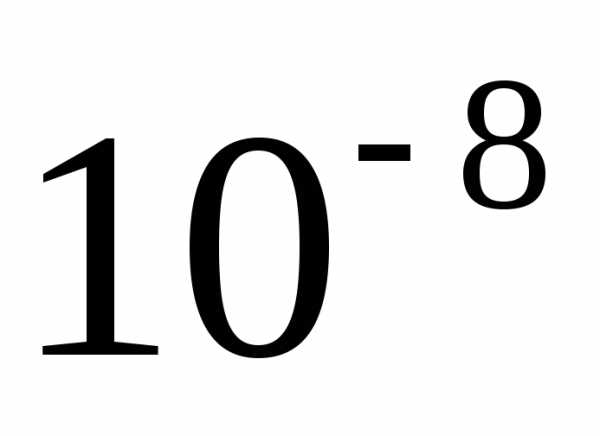 с, длина цугов ~3м. (Прерывистое излучение света атомами в виде коротких импульсов называется волновым цугом.) В следующие
с, длина цугов ~3м. (Прерывистое излучение света атомами в виде коротких импульсов называется волновым цугом.) В следующие с излучают другие атомы. Глаз воспринимает усредненную картину примерно за 0,1с. То, что фазы меняются и принимают случайные значения и обуславливает не когерентность источников.
с излучают другие атомы. Глаз воспринимает усредненную картину примерно за 0,1с. То, что фазы меняются и принимают случайные значения и обуславливает не когерентность источников.
Для получения когерентных источников волну разбивают на две части. Эти две получившиеся волны распространяются в оптических средах с разными показателями преломления 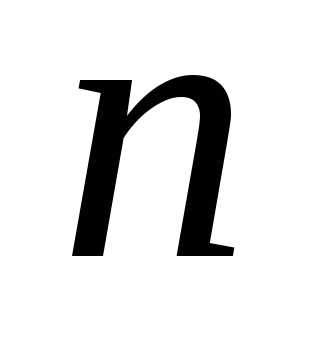 , а затем их соединяют. Если разность оптических путей не очень велика, складываемые волны принадлежат одному цугу, будет наблюдаться интерференция. (Оптическим путем называется произведения показателя преломления на геометрический путь
, а затем их соединяют. Если разность оптических путей не очень велика, складываемые волны принадлежат одному цугу, будет наблюдаться интерференция. (Оптическим путем называется произведения показателя преломления на геометрический путь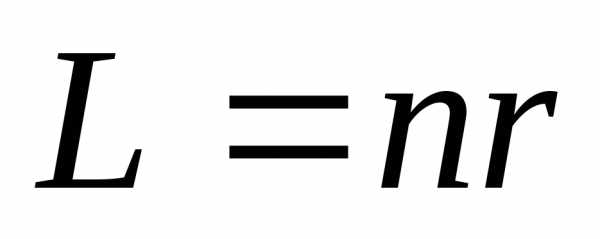 ).
).
|
Рис.1. |
Луч 1 разделили, одна часть идет по среде с показателем преломления 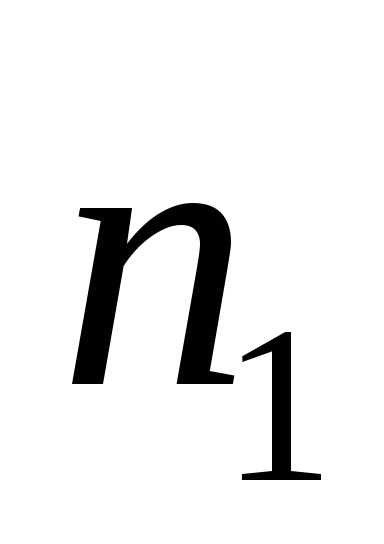 , другая по среде с
, другая по среде с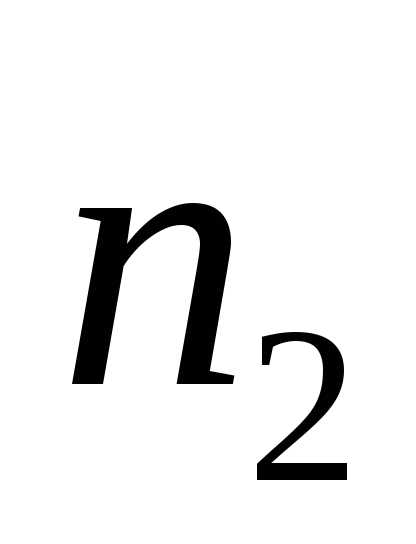 . В точке А они соединились:
. В точке А они соединились:
,.
Разность фаз равна: . Учитывая, что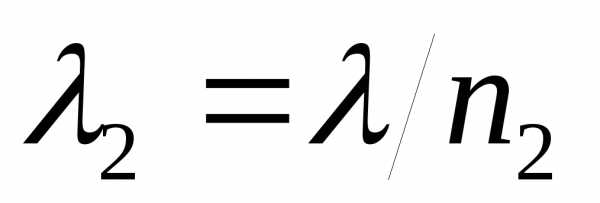 и
и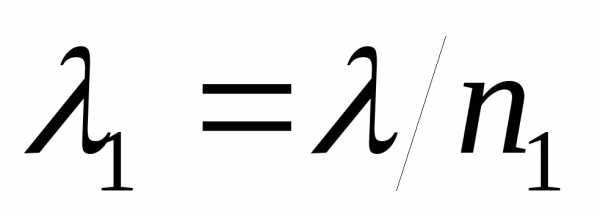 получаем:, где
получаем:, где - длина волны в вакууме, а
- длина волны в вакууме, а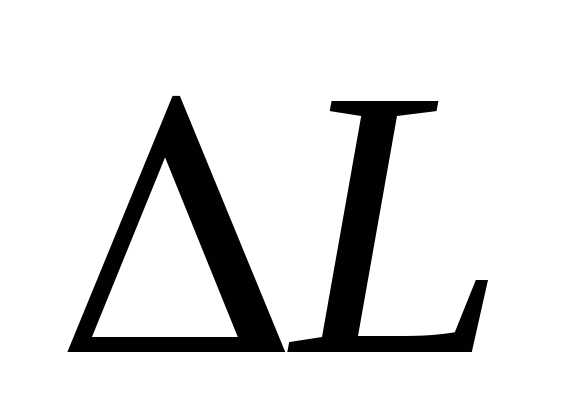 - оптическая разность хода.
- оптическая разность хода.
Найдем, при каких оптических разностях ходя будут наблюдаться интерференционные максимумы и минимумы. Максимумы наблюдаются при разностях фаз , где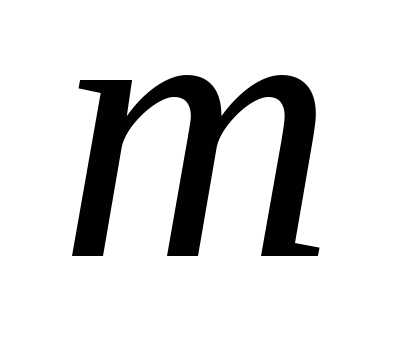 - целое. Следовательно
- целое. Следовательно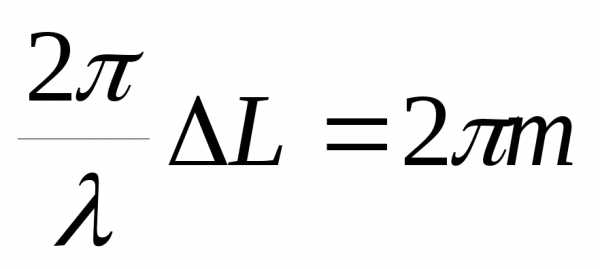 , отсюда
, отсюда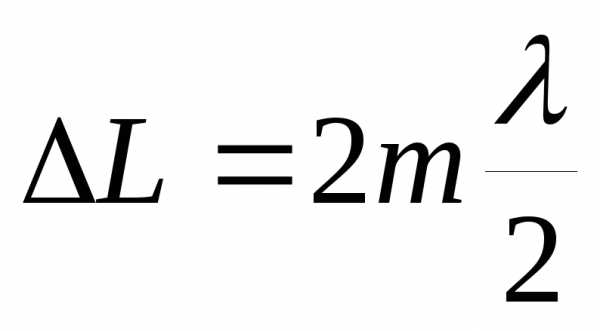 .
.
Если в оптической разности хода укладывается четное число полуволн, то наблюдается интерференционный максимум.
Минимум наблюдается при разности фаз или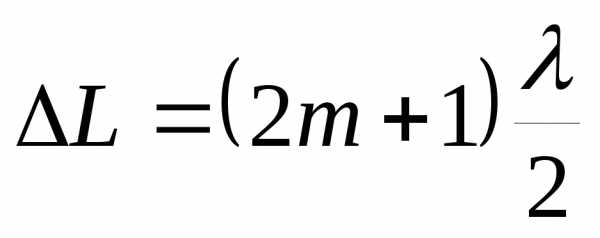 .
.
Если в оптической разности хода укладывается нечетное число полуволн, то наблюдается интерференционный минимум.
Расчет интерференции в опыте Юнга.
Впервые интерференцию света наблюдал Юнг. На пути распространения плоской волны он расположил щель. Эта щель играет роль точечного источника. Затем расположил экран с двумя щелями – это два когерентных источника. Они когерентны, так как волны идущие от них образовались от одной волны. На экране наблюдалось наложение волн – интерференция.
| Рис.2.
|
Интенсивность в любой точке А определяется оптической разностью хода:
, так как.
Из рисунка следует, что
,, тогда
, так как ,
,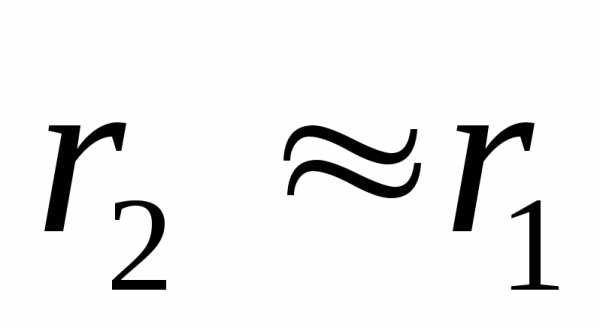 .
.
,
,
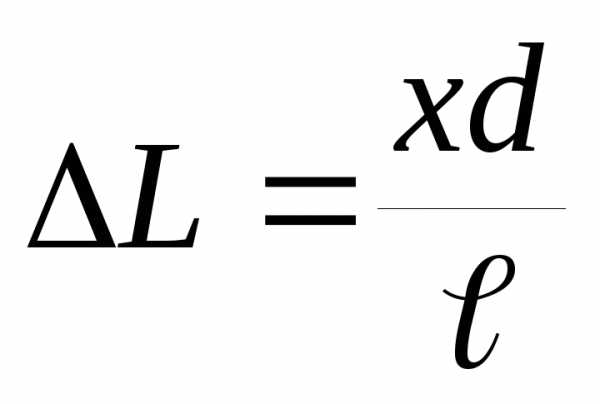 .
.
Найдем координаты максимумов:
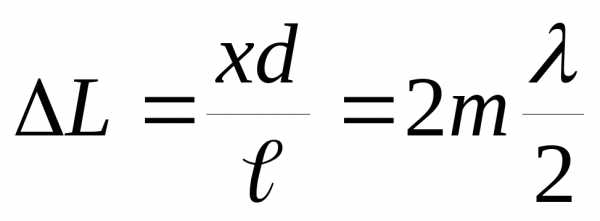 , отсюда
, отсюда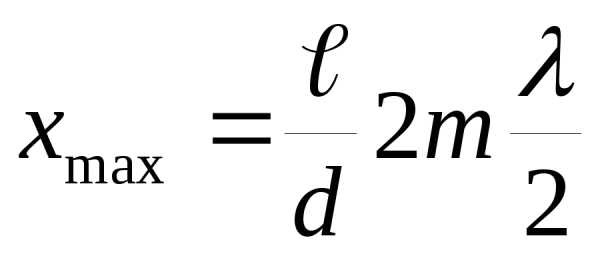 ,
,
координаты минимумов:
, отсюда.
Расстояние между соседними максимумами равно:
,
а между соседними минимумами:
.
Расстояние между соседним максимумом и минимумом:
Лекция 3. Интерференция света
Интерференция в тонких пленках
Явление интерференции в тонких пленках широко наблюдается в естественных условиях: радужная окраска мыльных пузырей, нефтяных пленок, масляных пятен на поверхности воды, крыльев бабочки.
В этом случае интерферируют лучи, полученные от отражения падающего луча от верхней и нижней поверхностей. Оптическая разность хода между лучами не велика из-за малой толщины пленки и поэтому они принадлежат одному цугу, а значит когерентны.
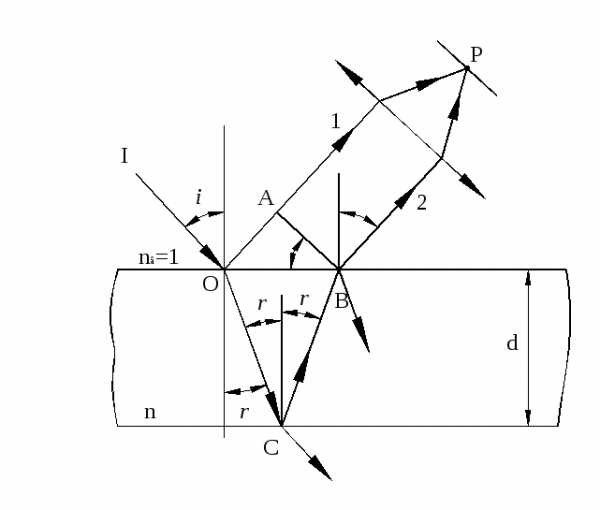
Для установления общих закономерностей интерференции света в тонких пленках рассмотрим плоскопараллельную прозрачную пленку толщиной  , на которую под углом
, на которую под углом =
=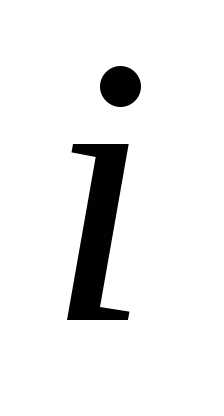 падает монохроматическая волна. Будем предполагать, что по обе стороны от пленки находиться воздух. Абсолютный показатель преломления пленки
падает монохроматическая волна. Будем предполагать, что по обе стороны от пленки находиться воздух. Абсолютный показатель преломления пленки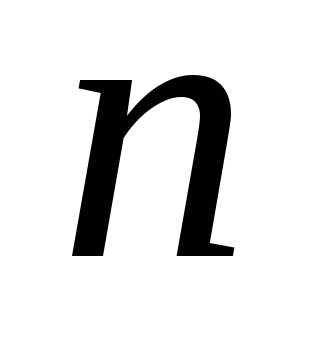 больше чем у воздуха.
больше чем у воздуха.
| Рис.1 |
Падающая волна частично отражается от поверхности пленки (луч 1) и частично преломляется (луч OC). Преломленная волна, достигнув нижней поверхности пленки, отражается от нее (лучCB). ЛучCBзатем преломляется на верхней поверхности (луч 2). Лучи 1 и 2 с помощью линзы собираются на экране в точке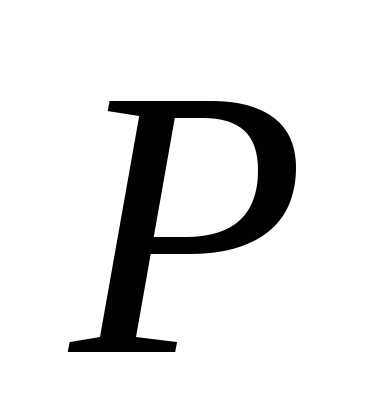 и интерферируют. Результат интерференции зависит от оптической разности хода между лучами 1 и 2.
и интерферируют. Результат интерференции зависит от оптической разности хода между лучами 1 и 2.
Оптическая разность хода между двумя интерферирующими лучами от точки Oдо плоскостиABравна:, где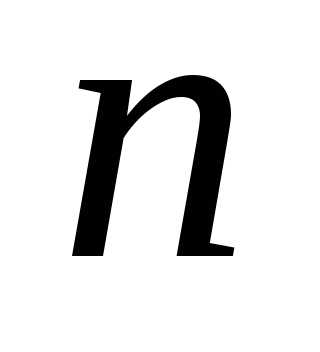 - показатель преломления пленки, член
- показатель преломления пленки, член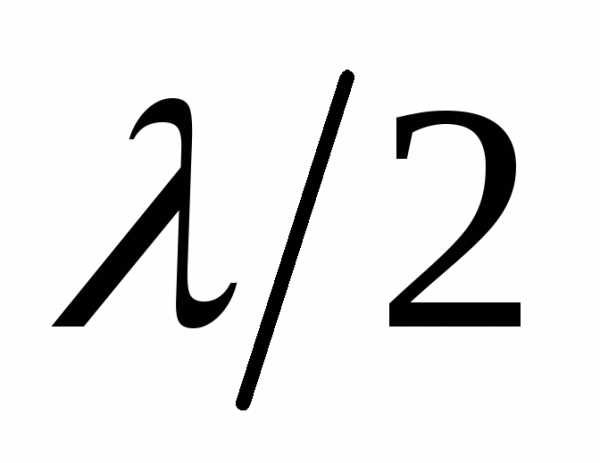 обусловлен потерей полуволны при отражении света от границы раздела с оптически более плотной средой. РасстоянияOA,OCиCBнаходится геометрическим методом (
обусловлен потерей полуволны при отражении света от границы раздела с оптически более плотной средой. РасстоянияOA,OCиCBнаходится геометрическим методом (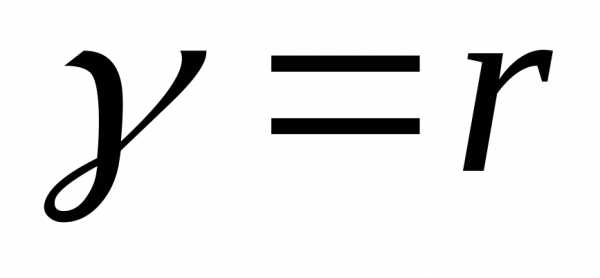 , рис.1):
, рис.1):
,.
Учитывая, что , получим:
.
Выразим оптическую разность хода через величину угла  . Учитывая, что, получим:
. Учитывая, что, получим:
.
Из этого выражения следует, что интерференционная картина в тонких пленках зависит от величин  ,
, ,
,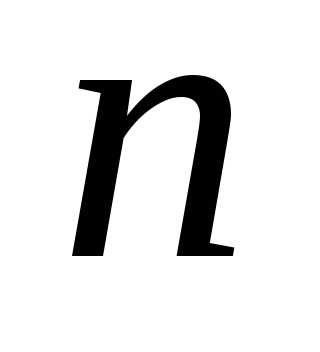 и
и . Для заданных
. Для заданных ,
, и
и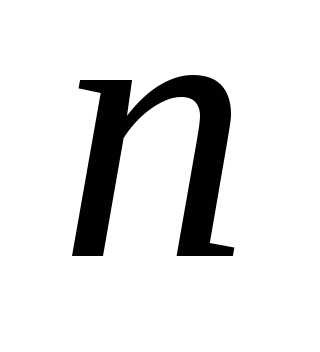 каждому наклону лучей
каждому наклону лучей соответствует своя интерференционная полоса. Интерференционные полосы, возникающие в результате наложения лучей падающих на плоско-параллельную пластинку под одинаковыми углами, называются полосами равного наклона (рис.2).
соответствует своя интерференционная полоса. Интерференционные полосы, возникающие в результате наложения лучей падающих на плоско-параллельную пластинку под одинаковыми углами, называются полосами равного наклона (рис.2).
| Рис.2. |
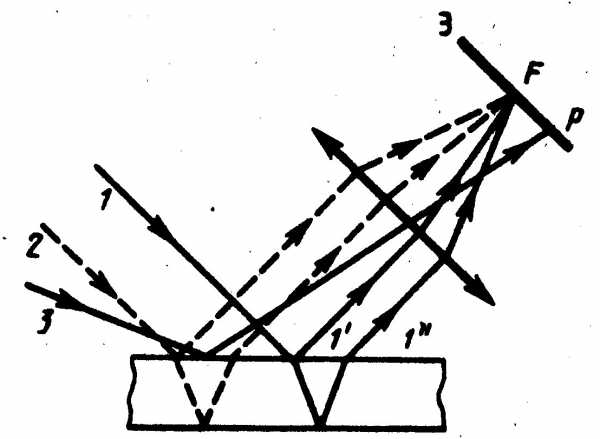
Интерференция на клине.
Полосы равной толщины получаются от пластинки переменной толщины. Пусть на клин (угол  между боговыми гранями мал) падает плоская волна, направление распространения которой совпадает с параллельными лучами 1 и 2 (рис.3).
между боговыми гранями мал) падает плоская волна, направление распространения которой совпадает с параллельными лучами 1 и 2 (рис.3).
| Рис.3. |
Падающий луч 1 разделяется на лучи  и
и , полученные отражением луча от верхней и нижней поверхности клина. После прохождения через линзу лучи пересекутся в точке
, полученные отражением луча от верхней и нижней поверхности клина. После прохождения через линзу лучи пересекутся в точке , являющейся изображением точки
, являющейся изображением точки . Лучи
. Лучи и
и когерентны и будут интерферировать в точке
когерентны и будут интерферировать в точке . При расчете оптической разности хода толщина клина берется в месте падения луча. Лучи
. При расчете оптической разности хода толщина клина берется в месте падения луча. Лучи и
и , образовавшиеся при делении луча
, образовавшиеся при делении луча , падающего в другую точку клина, собираются линзой в точке
, падающего в другую точку клина, собираются линзой в точке . Оптическая разность хода уже определяется толщиной
. Оптическая разность хода уже определяется толщиной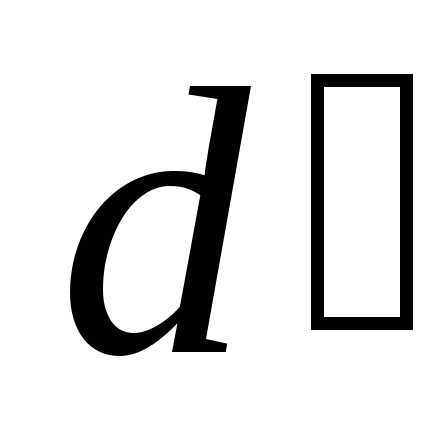 . Таким образом, на экране возникает система интерференционных полос. Каждая из полос возникает при отражении от мест пластинки, имеющих одинаковую толщину. Интерференционные полосы, возникающие в результате интерференции от мест одинаковой толщины, называются полосами равной толщины. Так как верхняя и нижняя грани клина не параллельны между собой то лучи
. Таким образом, на экране возникает система интерференционных полос. Каждая из полос возникает при отражении от мест пластинки, имеющих одинаковую толщину. Интерференционные полосы, возникающие в результате интерференции от мест одинаковой толщины, называются полосами равной толщины. Так как верхняя и нижняя грани клина не параллельны между собой то лучи и
и (
( и
и ) пересекаются вблизи пластинки.
) пересекаются вблизи пластинки.
Когда свет падает на кончик клина оптическая разность хода равна , так как . Поэтому кончик клина всегда темный луч 1 теряет
. Поэтому кончик клина всегда темный луч 1 теряет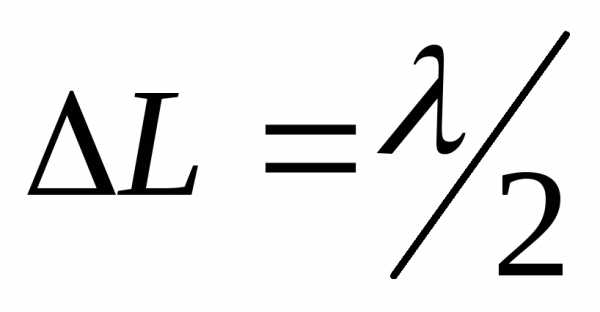 а луч2 не теряет
а луч2 не теряет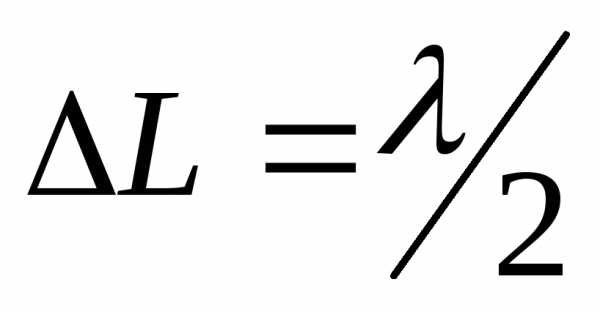 .
.
studfiles.net
Интерференция света
Интерференция в тонких пленках
Явление интерференции в тонких пленках широко наблюдается в естественных условиях: радужная окраска мыльных пузырей, нефтяных пленок, масляных пятен на поверхности воды, крыльев бабочки.
В этом случае интерферируют лучи, полученные от отражения падающего луча от верхней и нижней поверхностей. Оптическая разность хода между лучами не велика из-за малой толщины пленки и поэтому они принадлежат одному цугу, а значит когерентны.
Для установления общих закономерностей интерференции света в тонких пленках рассмотрим плоскопараллельную прозрачную пленку толщиной , на которую под углом = падает монохроматическая волна. Будем предполагать, что по обе стороны от пленки находиться воздух. Абсолютный показатель преломления пленки больше чем у воздуха.
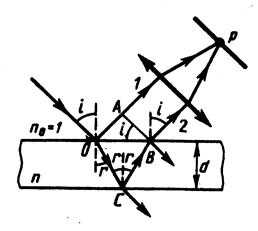 Рис.1
Рис.1
|
Падающая волна частично отражается от поверхности пленки (луч 1) и частично преломляется (луч OC). Преломленная волна, достигнув нижней поверхности пленки, отражается от нее (луч CB). Луч CB затем преломляется на верхней поверхности (луч 2). Лучи 1 и2 с помощью линзы собираются на экране в точке и интерферируют. Результат интерференции зависит от оптической разности хода между лучами 1 и 2.
Оптическая разность хода между двумя интерферирующими лучами от точки O до плоскости AB равна: , где - показатель преломления пленки, член обусловлен потерей полуволны при отражении света от границы раздела с оптически более плотной средой. Расстояния OA, OC и CB находится геометрическим методом ( , рис.1):
, .
Учитывая, что , получим:
.
Выразим оптическую разность хода через величину угла . Учитывая, что , получим:
.
Из этого выражения следует, что интерференционная картина в тонких пленках зависит от величин , , и . Для заданных , и каждому наклону лучей соответствует своя интерференционная полоса. Интерференционные полосы, возникающие в результате наложения лучей падающих на плоско-параллельную пластинку под одинаковыми углами, называются полосами равного наклона (рис.2).
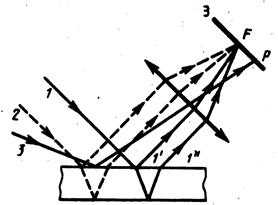 Рис.2.
Рис.2.
|
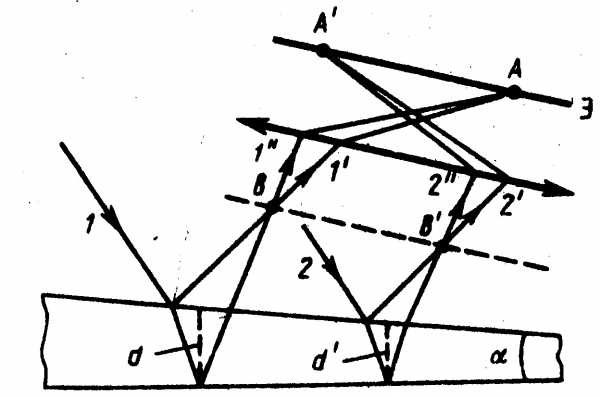
Полосы равной толщины получаются от пластинки переменной толщины. Пусть на клин (угол между боговыми гранями мал) падает плоская волна, направление распространения которой совпадает с параллельными лучами 1 и 2 (рис.3).
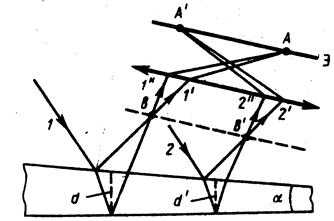 Рис.3.
Рис.3.
|
Падающий луч 1 разделяется на лучи и , полученные отражением луча от верхней и нижней поверхности клина. После прохождения через линзу лучи пересекутся в точке , являющейся изображением точки . Лучи и когерентны и будут интерферировать в точке . При расчете оптической разности хода толщина клина берется в месте падения луча. Лучи и , образовавшиеся при делении луча , падающего в другую точку клина, собираются линзой в точке . Оптическая разность хода уже определяется толщиной . Таким образом, на экране возникает система интерференционных полос. Каждая из полос возникает при отражении от мест пластинки, имеющих одинаковую толщину. Интерференционные полосы, возникающие в результате интерференции от мест одинаковой толщины, называются полосами равной толщины. Так как верхняя и нижняя грани клина не параллельны между собой то лучи и ( и ) пересекаются вблизи пластинки.
Когда свет падает на кончик клина оптическая разность хода равна , так как . Поэтому кончик клина всегда темный луч 1 теряет а луч2 не теряет .
Кольца Ньютона
Установка для наблюдения колец Ньютона состоит из плоско-параллельной пластины и плосковыпуклой линзы большого радиуса кривизны. Свет на установку падает вертикально (рис. 4).
| Рис. 4 |
Тонкая пленка образуется между линзой и пластинкой. Это воздушная пленка или жидкая. Пленка имеет вид клина. Поэтому возникают полосы равной толщины. Из-за симметрии они имеют вид окружностей.
Рассмотрим ход одного из лучей. Поскольку угол клина мал, можно считать, что угол падения везде ноль. Когерентными являются лучи, отразившиеся в точках 1 и 2. В точке 1 они накладываются. Найдем радиус -ого кольца .
Оптическая разность хода между лучами 1 и 2 равна: . В нашем случае , поэтому
.
Предположим, что кольцо темное, тогда . Отсюда выражаем толщину клина в точке кольца :
.
Из рис.4 следует, что . Пренебрегая членом , получаем:
.
Приравнивая оба выражения для , получаем: . Отсюда выражаем радиус -ого темного кольца:
.
Для воздушной пленки ( ), это выражение принимает вид: .
Найдем радиусы светлых колец. Оптическая разность хода в этом случае равна . Отсюда . Приравнивая с предыдущим выражением , получим:
.
Радиусы колец зависят от длины волны , поэтому, если свет немонохроматический, то кольца будут окрашены.
Применение интерференции
1. С помощью колец Ньютона можно определить длину волны, если известен радиус кривизны плосковыпуклой линзы ( ).
2. Явление интерференции применяется для улучшения качества оптических приборов (просветление оптики). Прохождение света через линзу сопровождается отражением 4% падающего света. Современные объективы содержат до 10 линз, поэтому потери света велики. Отражение от поверхности линз приводит к возникновению бликов, что приводит к демаскировке расположения приборов в военной технике. Для устранения этих недостатков осуществляют просветление оптики. Объектив покрывают пленкой. Ее толщину рассчитывают так, чтобы был интерференционный минимум при наложении лучей (рис. 5).
| Рис.5. |
Оптическая разность хода между лучами 1 и 2 равна . Слагаемое отсутствует, так как оба луча отражаются от более плотных поверхностей ( ). Пленка имеет наименьшую толщину при . Она равна: . Толщину подбирают так, чтобы гасить лучи наиболее сильно действующие на глаз (желто-зеленые). Объективы имеют фиолетовый оттенок.
Похожие статьи:
poznayka.org
2. Сложение световых волн. Интерференция. Оптическая разность хода. Условия максимума и минимума интерференционной картины.
Законы геометрической оптики. Явление полного отражения. Оптика-раздел физ. Кот изучает природу света, свет. явл. и взаимодействие света с веществом. Оптика делится на : геометрическую, волновую, квантовую.
Законы : 1.Закон прямолинейного распространения света: свет в оптической однородной среде распространяется прямолинейно. 2. Закон независимости свето. Пучков: эффект производимый одним пучком не зависит от того, действуют ли одновременно остальные пучки или они устранены. 3.Закон отражения: луч падающий, луч отраженный и перпендикулярный восстановленный к границу падения, лежат в оной Плоскости. 4. Закон преломления : луч падающий, луч преломленный и перпендикулярный восстановленный к границе падения лежат в одной плоскости.Линзы- прозрачное тело, ограниченное с двух сторон сферической поверхностью1. Двояковогнутый 2. Плоско-выгнутые 3. Вогнуто-выпуклая 4.Двояковыгнутая 5.Плосковыгнутая 6. Выпукло-вогнутая.
2. Сложение световых волн. Интерференция. Оптическая разность хода. Условия максимума и минимума интерференционной картины.
Интерференция-это явл. сложение в пространстве двух или нескольких поперечных волн при кот. В разных его точках получается усиление или ослабление амплитуды результирующих волн. Волны наз. когерентными, если 1)2) Разность фаз м/у колебаниями происходящие в каждую точку пространстваconst 
2 источника света перекрывающиеся в поле интерференции P. Они складываются в фазе(в этих местах max интенсивности эл.-маг. Поля)если в поле интереференции поместить непрозрачный экран, то будет наблюдаться интерференционная картинка. Когерентность волны означает, что в различных пространственных точках волны осцилляции происходят синхронно, то есть разность фаз между двумя точками не зависит от времени. Отсутствие когерентности, следовательно — ситуация, когда разность фаз между двумя точками не постоянна, а меняется со временем.Пространственная когерентность – хар. Разбросом направлений волнового вектора K. Она зависит от условий излучения и формирования световых волн. Представим что источники волн с одинаковыми началами фаз и длиной волны расположены на отрезке длины d, на кот. Наблюдается интерференция. Наблюдаемая картина может быть представлена как наложение интерференционных картин, создаваемых бесконечным множеством пар точечных источников. Временная когерентность волны характеризует сохранение взаимной когерентности при временном отставании одного из таких лучей по отношению к другому. Временной аспект когерентности имеет исключительно важное значение при рассмотрении явл. 1)монохроматические волны с одинаковыми частотами не сущ. Из за статического аспекта. 2) монохроматические волны представляет собой бесконечный пространственно-временной процесс.
5. Интерференция на тонких пленках. Полосы равного наклона. Полосы равной толщины. «Просветление» оптики.
Пусть монохроматическая волна падает на тонкую пpозpачную пленку, от которой она дважды отражается : часть от верхней поверхности пленки, часть - от нижней ее поверхности (а часть проходит через пленку). Эти две отваженные волны (а и b)когерентны и, накладываясь друг на друга, интеpфеpиpуют. 
Плоского равного наклона: Пленка имеет постоянную толщину, но на нее падает pасходящийся пучок света. Разность хода интеpфеpиpующих волн будет зависеть от угла падения лучей. Полосы максимумов и минимумов интеpфеpенции следуют тепеpь за постоянными углами падения. Чтобы их наблюдать необходимо собиpать лучи, отpаженные под одним и тем же углом, т. е. собиpать паpаллельные лучи. Поэтому глаз для наблюдения полос pавного наклона нужно сфокусиpовать на бесконечность. Говоpят, что полосы pавного наклона наблюдаются в бесконечности .Полосы равной толщины: пример на клине: в различных местах клина имеет различную разность хода отраженных лучей. Оптическая разность хода опр: Просветле́ние о́птики — это нанесение на поверхность линз, граничащих с воздухом, тончайшей плёнкиили нескольких плёнок одна поверх другой. Это необходимо для увеличения светопропускания оптической системы.
.Полосы равной толщины: пример на клине: в различных местах клина имеет различную разность хода отраженных лучей. Оптическая разность хода опр: Просветле́ние о́птики — это нанесение на поверхность линз, граничащих с воздухом, тончайшей плёнкиили нескольких плёнок одна поверх другой. Это необходимо для увеличения светопропускания оптической системы.
4. Методы наблюдения интерференции. Метод Юнга. Зеркала Френеля. Бипризма Френеля.
1)Опыт Юнга : Прошедший через щельS свет, в следствие дифракции образовал расходящийся пучок, кот. Падает на 2ой экран B . Пройдя щели S1 и S2 расположенные на одинаковом расстояние , волны в них перекрываются и создают интерференционную картинку. 2)Зеркала Френеля: 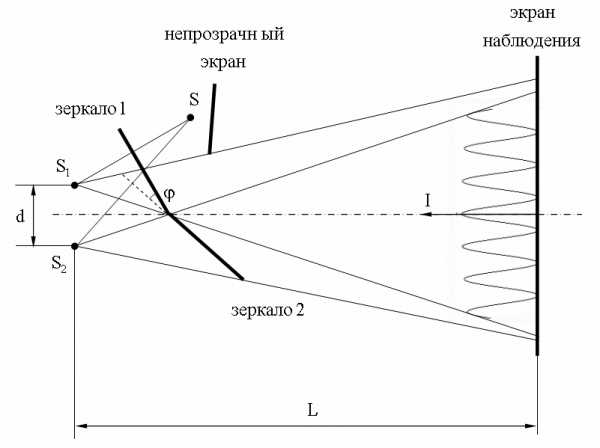 Две когерентные световые волны получаются в рез. Отражения от двух пластин наклоненные под небольшим углом друг к другу. Источником служит узкая ярко освещенная щель S отраженная от зеркал пучки падают на экран и перекрываются, возникает интерференционная картина. 3) Бипризма Френеля:
Две когерентные световые волны получаются в рез. Отражения от двух пластин наклоненные под небольшим углом друг к другу. Источником служит узкая ярко освещенная щель S отраженная от зеркал пучки падают на экран и перекрываются, возникает интерференционная картина. 3) Бипризма Френеля: 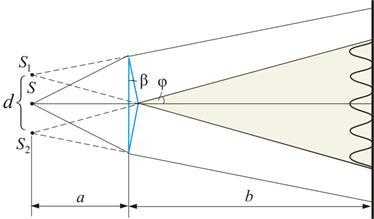 Для разделения исходной световой волны на две используют призму с углом близким к 180 градусов. Источником света служит ярко освещенная щель S, параллельная преломляющему ребру бипризмы. Образуются 2е близких мнимых изображения. 4) Зеркало Ллойда.
Для разделения исходной световой волны на две используют призму с углом близким к 180 градусов. Источником света служит ярко освещенная щель S, параллельная преломляющему ребру бипризмы. Образуются 2е близких мнимых изображения. 4) Зеркало Ллойда.
Прямой пучок света от источника S интерферирует с пучком, отражённым от зеркала под углом, близким к прямому. Таким образом, источниками когерентных волн являются источник S и его мнимое изображение в зеркале . При расчёте интерференционной картины следует учитыватьхарактер отражения света от поверхности зеркала.
6. Дифракция – огибание волнами краев протяженности.
Дифракция объясняется принципом Гюйгенса-Френеля. Каждая точка фронта волны является вторичным источником. Интерференция от вторичных источников дает дифракционную картину на экране.
Дифракция Френеля — дифракционная картина, которая наблюдается на небольшом расстоянии от препятствия, по условиям, когда основной вклад в интерференционную картину дают границы экрана.
Зоны Френеля.
Френели предложил разбить фронт волны на зоны, т.о. чтобы каждая следующая зона была отдалена от предыдущей на лямбда/2 дальше от точки Р. Обозначим амплитуды колебаний от первой, второй и т.д. зон
Амплитуда монотонно убывает по мере увеличения номера зоны
Дифракция в расходящихся пучках наз. дифракцией Френели. Дифракция в параллельных лучах наз. дифракцией Фраунгофера.
При прохождении света через узкую щель за нею получаются дифракционные полосы. Кроме того, происходит интерференция отдельных лучей. В зависимости от наклона лучей к оси симметрии системы получаются неодинаковые разности хода — чередование светлых и темных полос.
Каждому колебанию приходящему в точку М можно сопоставить вращающейся вектор. Выявим условия max и min используя метод векторных диаграмм. Разобьем ширину щели на n частей и каждому колебанию от участков сопоставим вектор
8. Дифракционная решетка. Расчет дифракционной картины от одномерной решетки. Дифракционная решетка как спектральный прибор. Дисперсия и разрешающая способность дифракционной решетки.
Дифракционная решетка – система параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками.
d – период диф.реш.
Дифракционная картина от диф.реш формируется в результате наложения двух эффектов:
Интерференция лучей, исходящих от одной щели
Интерференция N-лучей, исходящих N-щелей рабочей области диф.реш.
Дифракционная решетка как спектральный прибор
В состав видимого света входят монохроматические волны с различными значениями длин. В излучении нагретых тел (нить лампы накаливания) длины волн непрерывно заполняют весь диапазон видимого света. Такое излучение называется белым светом. Свет, испускаемый, например, газоразрядными лампами и многими другими источниками, содержит в своем составе отдельные монохроматические составляющие с некоторыми выделенными значениями длин волн. Совокупность монохроматических компонент в излучении называется спектром. Белый свет имеет непрерывный спектр, излучение источников, в которых свет испускается атомами вещества, имеетдискретный спектр. Приборы, с помощью которых исследуются спектры излучения источников, называются спектральными приборами.
Щель S, на которую падает исследуемое излучение, находится в фокальной плоскости линзы Л1. Эта часть прибора называется коллиматором. Выходящий из линзы параллельный пучок света падает на призму P. Вследствие дисперсии свет разных длин волн выходит из призмы под разными углами. В фокальной плоскости линзы Л2располагается экран или фотопластинка, на которой фокусируется излучение. В результате в разных местах экрана возникает изображение входной щели S в свете разных длин волн. У всех прозрачных твердых веществ (стекло, кварц), из которых изготовляются призмы, показатель преломления n в диапазоне видимого света убывает с увеличением длины волны λ, поэтому призма наиболее сильно отклоняет от первоначального направления синие и фиолетовые лучи и наименее – красные. Монотонно убывающая зависимость n (λ) называется нормальной дисперсией.
Первый опыт по разложению белого света в спектр был осуществлен И. Ньютоном (1672 г.).
В спектральных приборах высокого класса вместо призм применяются дифракционные решетки. Решетки представляют собой периодические структуры, выгравированные специальной делительной машиной на поверхности стеклянной или металлической пластинки (рис. 3.10.2). У хороших решеток параллельные друг другу штрихи имеют длину порядка 10 см, а на каждый миллиметр приходится до 2000 штрихов. При этом общая длина решетки достигает 10–15 см. Изготовление таких решеток требует применения самых высоких технологий. На практике применяются также и более грубые решетки с 50 – 100 штрихами на миллиметр, нанесенными на поверхность прозрачной пленки. В качестве дифракционной решетки может быть использован кусочек компакт-диска или даже осколок граммофонной пластинки.
Дисперсия и разрешающая способность дифракционной решетки.
Дисперсия света (разложение света) — это явление, обусловленное зависимостью абсолютного показателя преломления вещества от частоты (или длины волны) света (частотная дисперсия), или, то же самое, зависимость фазовой скорости света в веществе от длины волны (или частоты).
Разрешающая способность дифракционной решетки определяется общим числом штрихов и порядком спектра. Величина разрешающей способности может составлять сотни тысяч: единиц.
11. Свет, в котором направления колебаний светового вектора каким-то образом упорядочены, называется поляризованным. Одним из способов получения поляризованного света является его отражение и преломление на границе раздела двух изотропных диэлектриков. Если направить пучок естественного света на границу раздела двух диэлектриков (например, воздух – стекло), то часть света отражается, а часть, преломляясь, распространяется во второй среде. Располагая анализатор (например, кристалл турмалина) на пути луча, можно исследовать поляризации отраженного и преломленного лучей. Оказалось, что отраженный и преломленный лучи поляризованы частично, причем, в отраженном луче преобладают колебания, перпендикулярные к плоскости падения, а в преломленном луче – колебания, параллельные плоскости падения. Степень поляризации зависит от угла падения. При некотором строго определённом для данных сред значении угла падения отраженный от границы раздела свет оказывается полностью линейно – поляризованным. Такой угол падения называется углом Брюстера ( ίБр ) или углом полной поляризации и определяется согласно закону, установленному в 1815г Брюстером:
Зако́н Брю́стера — закон оптики, выражающий связь показателей преломления двух диэлектриков с таким углом падения света, при котором свет, отражённый от границы раздела диэлектриков, будет полностью поляризованным в плоскости, перпендикулярной плоскости падения.
Степенью поляризации (степень выделения световых волн с определенной ориентацией электрического (и магнитного) вектора) называется величина
Дисперсия света – явление зависимости показателя преломления света от длины волны.
Аномальная дисперсия - вид дисперсии света, при которой показатель преломления среды уменьшается с увеличением частоты световых колебаний. D>0
Нормальная дисперсия — это
дисперсия вдали от длин волн, при которых происходит поглощение света данным веществом. D<0
Поглощение света – уменьшение амплитуды колебаний при прохождении волны через какую-либо среду. Зако́н Бугера - физический закон, определяющий ослабление параллельного монохроматического пучка света при распространении его в поглощающей среде. 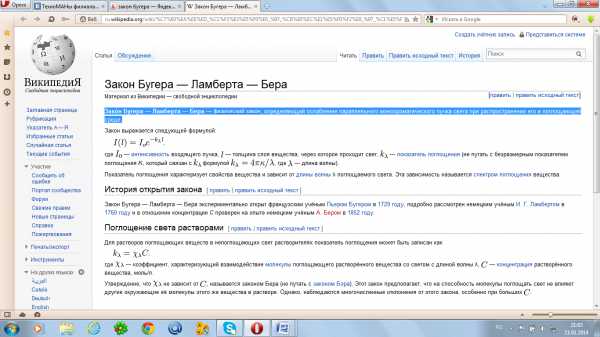 гдеI0 - интенсивность входящего пучка, l - толщина слоя вещества, через которое проходит свет, kλ - показатель поглощения. Показатель поглощения характеризует свойства вещества и зависит от длины волны λ поглощаемого света. Эта зависимость называется спектром поглощения вещества.
гдеI0 - интенсивность входящего пучка, l - толщина слоя вещества, через которое проходит свет, kλ - показатель поглощения. Показатель поглощения характеризует свойства вещества и зависит от длины волны λ поглощаемого света. Эта зависимость называется спектром поглощения вещества.
13) Трудности и противоречия классической физики. Тепловое излучение. Свойства теплового излучения и его основные характеристики: энергетическая светимость, спектральная плотность. Законы Кирхгофа, Стефана-Больцмана, Вина.
Тепловое излучение – электромагнитное излучение, которое совершается за счет энергии теплового движения атомов и молекул. Имеет сплошной спектр, максимум которого зависит от температуры тела. При остывании последний смещается в длинноволновую часть спектра.
Количественной характеристикой теплового излучения служит спектральная плотностьэлектрической светимости (испускательная способность тела) обозначается 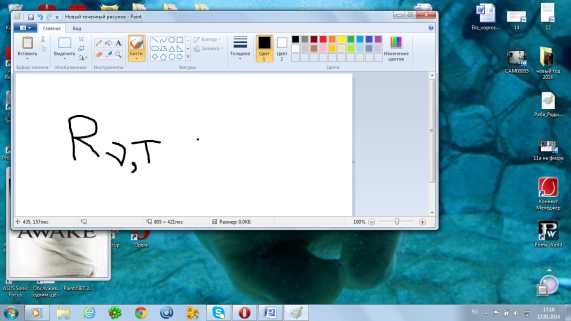 - это энергия излучения с единицы площади поверхности за единицу времени в единичном интервале частот.
- это энергия излучения с единицы площади поверхности за единицу времени в единичном интервале частот.
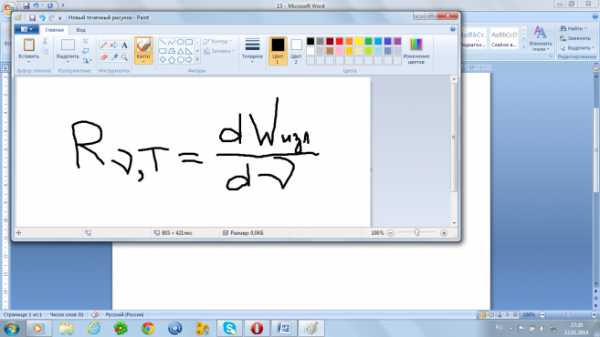 испускательная способность
испускательная способность
Энергия, излучаемая с единицы поверхности тела за единицу времени во всем диапазоне частот называется энергетическая светимость.
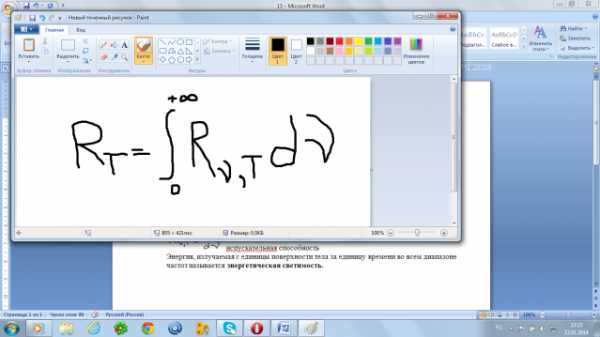 энергетическая светимость,
энергетическая светимость,
Способность тел поглощать падающее излучение, характеризуется поглащательной способностью.
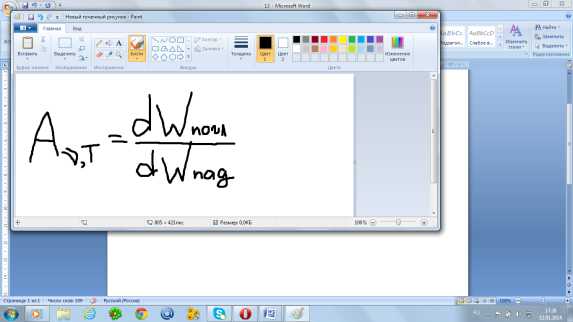 поглощающая способность
поглощающая способность
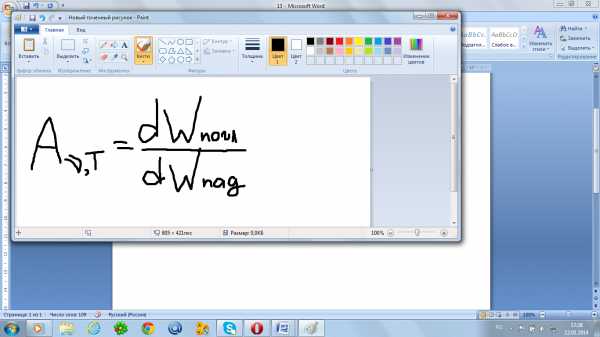 энергия, поглощаемая единицей поверхности за единицу времени в интервале частот от
энергия, поглощаемая единицей поверхности за единицу времени в интервале частот от  до
до
 энергия, падающая на единицу поверхности за единицу времени в интервале частот от
энергия, падающая на единицу поверхности за единицу времени в интервале частот от 
Закон Кирхгофа Определяет отношение между испускательной и поглащательной способности тел. отношение испускательной и поглащательной способностей тела не зависят от природы тела и являются универсальной функцией частоты и температуры. Rν,T/Aν,T=rν,Trν,T – универсальная ф-я Кирхгофа Aartν,T = Aart = 1
rν,T = Rartν,T
Закон Стефана-Больцмана
Энергетическая светимость art пропорциональна 4 степени абсолютной температуры.
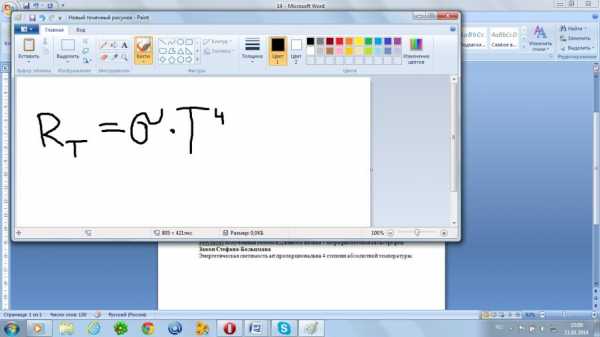
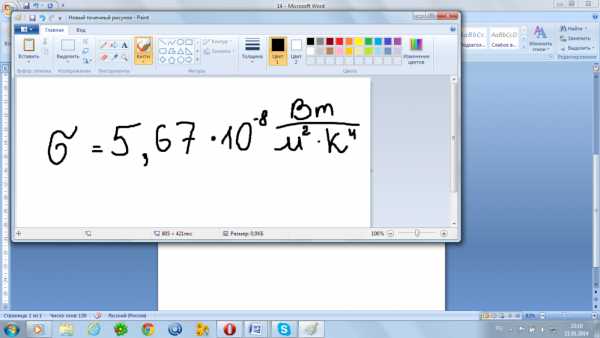 постоянная Стефана Больцмана
постоянная Стефана Больцмана
Закон смещения Вина
Длина волны, соответствующая максимуму испускательной способности art обратно пропорциональна абсолютной температутре.
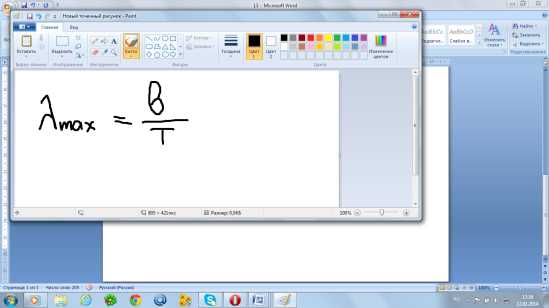 ;
; 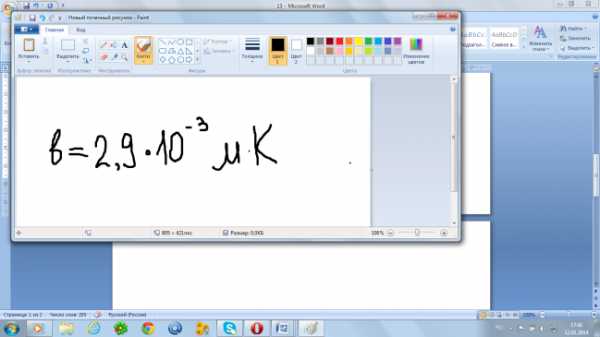 постоянная Вина
постоянная Вина
studfiles.net
Оптическая разность хода световых волн, возникающая при отражении монохроматического света от тонкой пленки
или
где d — толщина пленки; n — показатель преломления пленки; i — угол падения; r — угол преломления света в пленке.
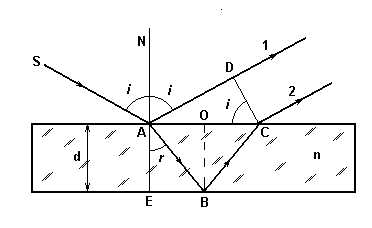
Если зафиксировать угол падения i и взять плёнку переменной толщины, то для определённых участков с толщиной d реализуются интерференционные полосы равной толщины.Эти полосы можно получить, если направить параллельный пучок света на пластинку с разной толщиной в разных местах.
Если на плоскопараллельную пластинку (d = const) направить расходящийся пучок лучей (т.е. пучок, который обеспечит различные углы падения i), то при наложении лучей, падающих под определенными одинаковыми углами, будут наблюдаться интерференционные полосы, которые называют полосами равного наклона
Классический пример полос равной толщины – кольца Ньютона. Они образуются, если на плосковыпуклую линзу, лежащую на стеклянной пластине, направить монохроматический пучок света. Кольца Ньютона представляют собой интерференционные полосы от областей с равной толщиной воздушного промежутка между линзой и пластинкой.
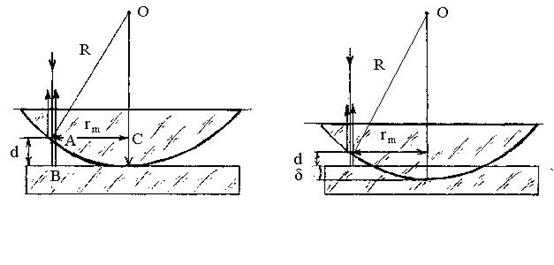
Радиус светлых колец Ньютона в отраженном свете
,
где k=1, 2, 3 …… — номер кольца; R — радиус кривизны.
Радиус темных колец Ньютона в отраженном свете
, где k=0, 1, 2, 3 …….
Похожие статьи:
poznayka.org
Расчет разности хода для лучей, отраженных от тонкой прозрачной пластинки
Расчет разности хода для лучей, отраженных от тонкой прозрачной пластинки, при соблюдении условий временной и пространственной когерентности.
Пусть на прозрачную плоскопараллельную пластинку падает плоская световая волна, которую можно рассматривать как параллельный пучок лучей. Пластинка отбрасывает вверх два параллельных пучка света. Один образован за счет отражения от верхней поверхности пластинки, второй как отражение от нижней поверхности (рис.) Пучки, прошедшие через пластинку нас не интересуют.
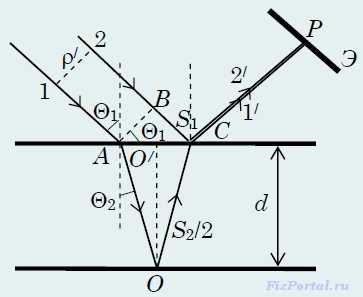 Разность хода, приобретенная лучами 1 и 2 до того, как они сойдутся в точке С равна Обозначим BC = S1, AO + OC = S2. Из треугольника ABC: O/C найдем из треугольника OO/C: Откуда Из треугольника OO/C: А поскольку то В точке С происходит отражение луча 2 от границы раздела среды, оптически менее плотной, со средой, оптически более плотной, в результате чего между лучами 1 и 2 возникает дополнительная разность фаз, равная π. Ее можно учесть, прибавив половину длины волны в вакууме в выражении (1) к ВС. В результате получим оптическую разность хода Δ для отраженных лучей 1/ и 2/: Итак, при падении на пластинку плоской волны образуются две отраженные волны, разность хода которых определяется формулой (2). Выясним условия, при которых эти волны окажутся когерентными и смогут интерферировать. Отраженные волны 1/ и 2/ смогут интерферировать, если соблюдены условия как временной, так и пространственной когерентности. Для того, чтобы имела место временная когерентность, разность хода Δ не должна превышать длину когерентности. Или Пренебрежем 1/2 по сравнению с λ0/Δλ0, а также примем Тогда получим Если λ0 = 0,5 мкм, а Δλ0 = 20 × 10−10 м, то d < 0,062 мм. Теперь рассмотрим условия соблюдения пространственной когерентности. Поставим на пути отраженных лучей экран Э (рис.) Приходящие в точку P лучи 1/ и 2/ отстоят в падающем пучке на расстояние ρ/. Если это расстояние не превышает радиуса когерентности ρког падающей волны, лучи 1/ и 2/ будут когерентными. Из рис. Видно, что Примем n = 1,5, Θ1 = 45, тогда ρ/ = 0,047 мм ≈ 0,05 мм. Таким образом, вследствие ограничений, накладываемых условиями временной и пространственной когерентности, интерференция при освещении пластинки солнечным светом наблюдается только в том случае, если толщина пластинки не превышает нескольких сотых миллиметра. При освещении светом с большей степенью когерентности интерференция наблюдается при отражении от более толстых пластинок.
Разность хода, приобретенная лучами 1 и 2 до того, как они сойдутся в точке С равна Обозначим BC = S1, AO + OC = S2. Из треугольника ABC: O/C найдем из треугольника OO/C: Откуда Из треугольника OO/C: А поскольку то В точке С происходит отражение луча 2 от границы раздела среды, оптически менее плотной, со средой, оптически более плотной, в результате чего между лучами 1 и 2 возникает дополнительная разность фаз, равная π. Ее можно учесть, прибавив половину длины волны в вакууме в выражении (1) к ВС. В результате получим оптическую разность хода Δ для отраженных лучей 1/ и 2/: Итак, при падении на пластинку плоской волны образуются две отраженные волны, разность хода которых определяется формулой (2). Выясним условия, при которых эти волны окажутся когерентными и смогут интерферировать. Отраженные волны 1/ и 2/ смогут интерферировать, если соблюдены условия как временной, так и пространственной когерентности. Для того, чтобы имела место временная когерентность, разность хода Δ не должна превышать длину когерентности. Или Пренебрежем 1/2 по сравнению с λ0/Δλ0, а также примем Тогда получим Если λ0 = 0,5 мкм, а Δλ0 = 20 × 10−10 м, то d < 0,062 мм. Теперь рассмотрим условия соблюдения пространственной когерентности. Поставим на пути отраженных лучей экран Э (рис.) Приходящие в точку P лучи 1/ и 2/ отстоят в падающем пучке на расстояние ρ/. Если это расстояние не превышает радиуса когерентности ρког падающей волны, лучи 1/ и 2/ будут когерентными. Из рис. Видно, что Примем n = 1,5, Θ1 = 45, тогда ρ/ = 0,047 мм ≈ 0,05 мм. Таким образом, вследствие ограничений, накладываемых условиями временной и пространственной когерентности, интерференция при освещении пластинки солнечным светом наблюдается только в том случае, если толщина пластинки не превышает нескольких сотых миллиметра. При освещении светом с большей степенью когерентности интерференция наблюдается при отражении от более толстых пластинок. Смотрите еще:Дисперсия света. Аномальная дисперсия.Группа волн.Расчет разности хода для лучей, отраженных от тонкой прозрачной пластинкиПолосы равной толщины и равного наклона.Кольца Ньютона.Принцип Гюйгенса-Френеля.Метод зон Френеля.
В практикум абитуриентаВ учебник по теорииЗадачи на интерференцию для самостоятельной работыВ банк задач абитуриентаfizportal.ru


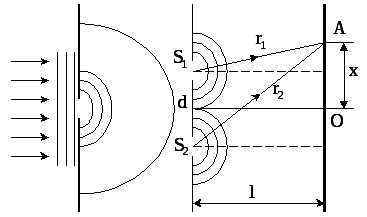
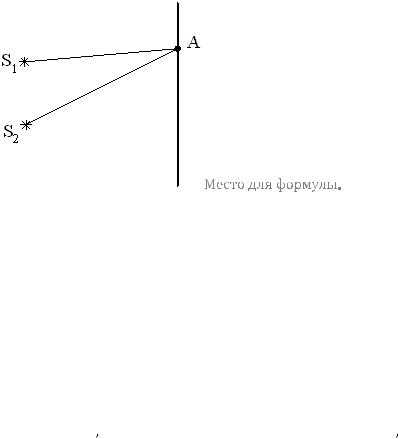
 - расстояние между источниками,
- расстояние между источниками,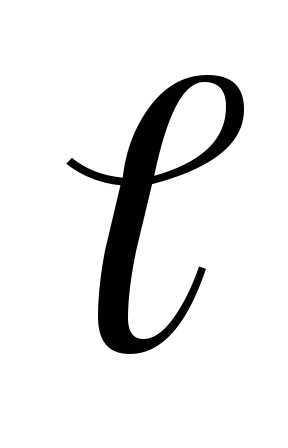 - расстояние от источников до экрана,
- расстояние от источников до экрана,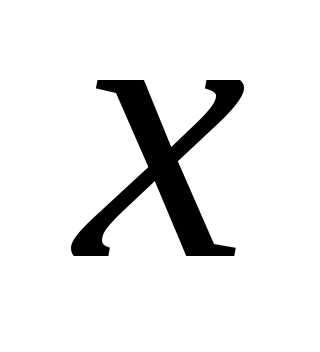 - расстояние от точки О до рассматриваемой точки А.
- расстояние от точки О до рассматриваемой точки А.