Интерференция при отражении от тонких пластинок. При отражении от тонкой пленки интерферируют световые пучки
Интерференция при отражении от тонких пластинок — МегаЛекции
При падении световой волны на тонкую прозрачную пластинку или пленку происходит отражение от обеих поверхностей пластинки. В результате возникают две световые волны, которые могут интерферировать. На пластинке происходит деление амплитуды, поскольку фронты волн на ней сохраняются, меняя лишь направление своего движения.
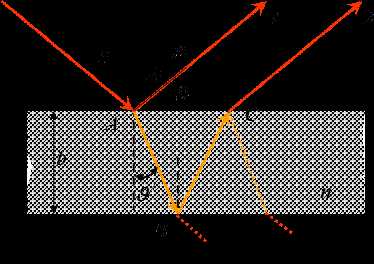
Пусть на прозрачную плоскопараллельную пластинку под углом (тета) относительно нормали к пластинке падает плоская световая волна, которую можно рассматривать как параллельный пучок лучей. Пластинка отражает вверх два параллельных пучка света, один из которых образовался за счет отражения от верхней поверхности пластинки, другой – от нижней поверхности. Кроме этих двух пучков пластинка отбросит вверх и другие пучки, которые возникают в результате трех, пятикратного и т.д. отражения от поверхностей пластинки. Однако эти пучки имеют малую интенсивность, в связи, с чем их вклад в интерференционную картину невелик.
Амплитуды двух рассматриваемых пучков света (волн) мало отличаются друг от друга, что важно для получения контрастной картины интерференции. Определим оптическую разность хода отраженных волн 1 и 2.
– показатель преломления среды.
Избавимся от , и . Из геометрических соображений можно записать: ; , , следовательно, , тогда . В этих выражениях – толщина пластинки. В итоге получим:
.
Из закона преломления следует, что . Подставив это соотношение в предыдущую формулу, получим
В полученном выражении необходимо учесть, что при отражении волны от оптически более плотной среды (в рассматриваемом случае от верхней поверхности пластинки) ее фаза изменяется скачком на величину . Этот вопрос мы рассматривали в разделе волны. Возникающую дополнительную разность фаз можно учесть, добавив к или вычтя из нее половину длины волны в вакууме. В результате получим:
.
Избавимся от угла : , следовательно,
.
Итак, при падении на пластинку плоской волны образуются две отраженные волны, разность хода которых определяется полученной формулой. Теперь важно определить условия, при которых волны окажутся когерентными и смогут интерферировать. Волны смогут интерферировать, если наблюдается временная и пространственная когерентность.
а) Условие временной когерентности.
Для обеспечения временной когерентности разность хода не должна превышать длину когерентности . Запишем это условие:
.
Это означает, что для толщины пластинки должно выполняться условие:
.
Упростим выражение. Пренебрежем по сравнению с . Учтем также, что имеет величину порядка единицы. Тогда условие временной когерентности можно записать в следующем виде.
, или – удвоенная толщина пластинки должна быть меньше длины когерентности. Пусть =0,5мкм, =0,02мкм. Предельное значение толщины пластинки при этом около 0,06 мм.
б) Условие пространственной когерентности.
Вспомним, что пространственная когерентность световой волны характеризуется параметром, который называется шириной когерентности . Это величина, пропорциональная отношению длины волны к угловому размеру источника светового излучения: . Отраженные от верхней и нижней поверхностей пластинки лучи будут интерферировать в том случае, если расстояние между лучами не превышает половины ширины когерентности: . Запишем условие пространственной когерентности без вывода.
Выполнение этого условия будет зависеть от угла падения лучей . Чем меньше угол падения, тем меньше и менее существенным становится для получения интерференционной картины параметр источника светового излучения.
Таким образом, волны будут интерферировать, если выполняются записанные условия временной и пространственной когерентности. Интерференционная картина будет наблюдаться в виде системы полос, причем при будут наблюдаться максимумы, а при – минимумы. Подставив в эти условия выражение для , получим для максимумов в отражённом свете.
,
и для минимумов .
Интерференционную картину при отражении световых лучей от тонких пленок обычно наблюдают с помощью линзы, в фокальной плоскости которой располагается экран. Линза не изменяет оптической разности хода между лучами и, следовательно, не изменяет разности фаз, но собирает в одну точку лучи падающие под одним углом на пластинку. На экране наблюдается система чередующихся светлых и темных круговых полос. Каждая полоса будет образована лучами, падающими на пластинку под одинаковым углом . В связи с этим интерференционные полосы называются полосами равного наклона. Локализованы полосы равного наклона в бесконечности.
Если использовать параллельный пучок света ( ), то разность хода лучей D для всех лучей будет одинаковой и чередующиеся темные и светлые полосы не будут наблюдаться. Будет одинаково освещённый экран, соответствующий максимуму или минимуму (или промежуточному значению) интерференции.
Все рассуждения были проведены нами для отраженного света. Интерференцию можно наблюдать и в проходящем свете. Особенность – в проходящем свете потери полуволны не наблюдается, оптическая разность хода волн для проходящего и отраженного света отличается на . В связи с этим, например, максимуму интерференции в отраженном свете соответствует минимум в проходящем свете.
Максимум.
Минимум.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Интерференция света в тонких пленках
В природе часто можно наблюдать окрашивание тонких пленок (масляные пленки на воде, мыльные пузыри, оксидные пленки на металлах), возникающие в результате интерференции света, отраженного двумя поверхностями пленки.
Пластинка постоянной толщины. При падении световой волны на тонкую прозрачную пластинку (или пленку) происходит отражение от обеих поверхностей пластинки. В результате возникают две световые волны, которые при определенных условиях могут интерферировать.
В результате отражений от поверхностей пластинки, часть света возвращается в исходную среду. Отраженный свет состоит из лучей, испытавших одно-, трех-, пяти- и т.д. кратное отражение. Ввиду малой интенсивности лучи трехкратного отражения и выше принимать в расчет не будем (при n=1,5 от поверхности пластинки отражается примерно 4 % падающего светового потока). Однократно отраженные от пластинки лучи 1 и 2 когерентны, если оптическая разность их хода меньше длины когерентности падающей волны. Если на пути лучей поставить собирающую линзу, то на экране, совмещенном с фокальной плоскостью линзы, возникнет интерференционная картина. Роль линзы может играть хрусталик, а экрана - сетчатка глаза. В этом случае глаз должен быть аккомодирован (наведен на резкость) на бесконечность.
Оптическая разность хода, возникающая между двумя интерферирующими лучами от точки O до точки P
.
Согласно рисунку (18.5)
, .
Учитывая закон преломления
,
получим
.
При вычислении разности колебаний в лучах 1 и 2 нужно, кроме оптической разности хода D¢, учесть возможность изменения фазы волны при отражении. В точке O отражение происходит от оптически более плотной среды. Поэтому фаза отраженной волны изменяется на p (для определенности считаем, что происходит потеря полуволны). В точке C отражение происходит от оптически менее плотной среды, так что скачка фазы не происходит. С учетом потери полуволны для оптической разности хода получим
. (18.3.1)
В точке P будет интерференционный максимум, если
, (18.3.2.,а)
и минимум, если
. (18.3.2.,б)
Выясним условия, при которых эти волны окажутся когерентными и смогут интерферировать. Для того, чтобы имела место временная когерентность, разность хода (18.3.1) не должна превышать длину когерентности . Следовательно, должно выполнятся условие
.
В рассеянном свете имеются лучи самых разнообразных направлений. Лучи, параллельные некоторому направлению, после отражения соберутся в одной точке и создадут в ней освещенность, определяемую значением оптической разности хода. Лучи, идущие в другом направлении, соберутся в другой точке и т.д. В результате возникает система чередующихся светлых и темных полос (если линза параллельна пластинке, полосы имеет вид концентрических колец с центром в фокусе линзы). Каждая полоса образована лучами, падающими на пластинку под одинаковым углом. Поэтому получающиеся интерференционные полосы носят название полос равного наклона.
Согласно формуле (18.3.2.,а) положение максимумов зависит от длины волны . Поэтому в белом свете интерференционная картина приобретает радужную окраску. Возможность наблюдения интерференционной картины в белом свете определяется способностью глаза различать оттенки цвета.
Кольца Ньютона. Классическим примером полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от соприкасающихся друг с другом толстой плоскопараллельной стеклянной пластинки и плоско-выпуклой линзы с большим радиусом кривизны (рис.18.6.).
,
где R – радиус кривизны линзы, r – радиус окружности, которой соответствует зазор толщины d. Таким образом,
.
С учетом потери полуволны, возникающей при отражении от пластинки, оптическая разность хода лучей равна
.
Используя условия максимума (18.3.2.,а) и минимума (18.3.2.,б), получим выражения для радиусов m-го светлого и m-го темного кольца соответственно
, (18.3.4.,а) . (18.3.4.,б)
Похожие статьи:
poznayka.org
12.Интерференция света при отражении от тонких пластинок. Полосы равной толщины и равного наклона.
Большой практический интерес представляет интерференция в тонких пластинках и пленках.
Пусть на тонкую плоскопараллельную пластину толщиной b, изготовленную из прозрачного вещества с показателем преломления n, из воздуха (nвозд » 1) падает плоская световая волна, которую можно рассматривать как параллельный пучок лучей (рис.4), под углом Q1 к перпендикуляру.
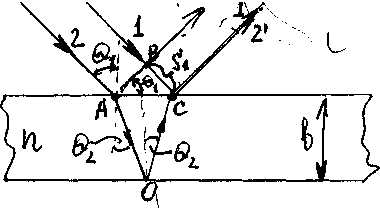
Рис.4.
На поверхности пластины в точке А луч разделится на два параллельных луча света, из которых один образуется за счет отражения от верхней поверхности пластинки, а второй – от нижней поверхности. Разность хода, приобретаемая лучами 1 и 2 до того, как они сойдутся в точке С, равна
D = nS2 – S1 ± l0/2
где S1 - длина отрезка АВ, а S2 – суммарная длина отрезков АО и ОС, а член ± l0/2 обусловлен потерей полуволны при отражении света от границы раздела двух сред с различными показателями преломления (n >nв –точка С) .
Из геометрического рассмотрения получается формула для оптической разности хода дучей1и2:
D' = 2bÖ(n2 – sin2Q1) = 2bn соsQ2,
ас учетом потери полуволны для оптической разности хода получим
D = 2bÖ(n2 – sin2Q1) ± l0/2 = 2bn соsQ2 ± l0/2. (10)
Вследствие ограничений, накладываемых временной и пространственной когерентностью, интерференция при освещении пластинки например солнечным светом наблюдается только в том случае, если толщина пластинки не превышает нескольких сотых миллиметра. При освещении светом с большей степенью когерентности (например, лазером) интерференция, наблюдается и при отражении от более толстых пластинок или пленок.
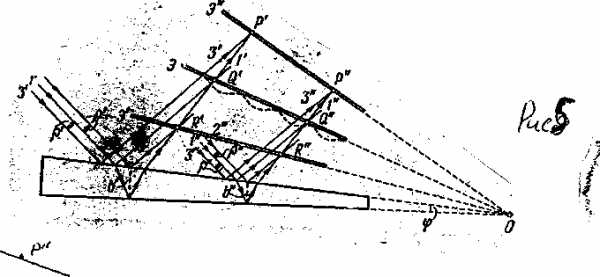
Практически интерференцию от плоскопараллельной пластинки наблюдают, поставив на пути отраженных пучков линзу, которая собирает лучи в одной из точек экрана, расположенного в фокальной плоскости линзы (рис.5). Освещенность в произвольной точке Р экрана зависит от значения величины D, определенной по формуле (10). При D = mlо получаются максимумы, при D = (m + 1/2)lо - минимумы интенсивности (m - целое число).
Пусть тонкая плоскопараллельная пластинка освещается рассеянным монохроматическим светом (рис.5). Расположим параллельно пластинке линзу, в фокальной плоскости которой поместим экран. В рассеянном свете имеются лучи самых разнообразных направлений. Лучи, параллельные плоскости рисунка и падающие на пластинку под углом Q'1, после отражения от обеих поверхностей пластинки соберутся линзой в точке Р и создадут в этой точке освещенность, определяемую значением оптической разности хода.
E
Рис.5.
Лучи, идущие в других плоскостях, но падающие на пластинку под тем же углом Q1¢ соберутся линзой в других точках, отстоящих от центра экрана О на такое же расстояние, как и точка Р. Освещенность во всех этих точках будет одинакова. Т.о. лучи, падающие на пластинку под одинаковым углом Q1¢, создадут на экране совокупность одинаково освещенных точек, расположенных по окружности с центром в точке О. Аналогично, лучи, падающие под другим углом Q"1 создадут на экране совокупность одинаково (но иначе, поскольку Δ иная) освещенных точек, расположенных по окружности другого радиуса.
В результате на экране возникнет система чередующихся светлых и темных круговых полос с общим центром в точке O). Каждая полоса образована лучами, падающими на пластинку под одинаковым углом Q1. Поэтому получающиеся в описанных условиях интерференционные полосы носят назв. полос равного наклона. При ином расположении линзы относительно пластинки (экран во всех случаях должен совпадать с фокальной плоскостью линзы) форма полос равного наклона будет другой. Роль линзы может играть хрусталик глаза, а экрана - сетчатка глаза.
Согласно (10) положение максимумов зависит от lо. Поэтому в белом свете получается совокупность смещенных др. относительно др. полос, образованных лучами разных цветов, и интерференционная картина приобретает радужную окраску.
Интерференционная картина от тонкого прозрачного клина переменной толщины была изучена еще Ньютоном. Пусть на такой клин (рис.6) падает параллельный пучок лучей.
Теперь лучи, отразившиеся от разных поверхностей клина, не будут параллельными. Но и в этом случае отраженные волны будут когерентными во всем пространстве над клином, и при любом расстоянии экрана от клина на нем будет наблюдаться интерференционная картина в виде полос, параллельных вершине клина 0. Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, вследствие чего их называют полосами равной толщины. Практически полосы равной толщины наблюдают, поместив вблизи клина линзу и за ней экран. Роль линзы может играть хрусталик, а роль экрана - сетчатка глаза. При наблюдении в белом свете полосы будут окрашенными, так что поверхность пластинки или пленки представляется имеющей радужную окраску. Такую окраску имеют, например, расплывшиеся по поверхности воды тонкие пленки нефти и масла, а также мыльные пленки. Заметим, что интерференция от тонких пленок может наблюдаться не только в отраженном, но и в проходящем свете.
studfiles.net
Лекции по оптике / L3-03
7
Л3-3Интерференция света в тонких пленках
Пластинка постоянной толщины.При падении световой волны на тонкую прозрачную пластинку (или пленку) происходит отражение от обеих поверхностей пластинки. В результате возникают две световые волны, которые при определенных условиях могут интерферировать.
Пусть на прозрачную плоскопараллельную пластинку падает плоская световая волна (параллельный пучок света). В результате отражений от поверхностей пластинки, часть света возвращается в исходную среду. Отраженный свет состоит из лучей, испытавших одно-, трех-, пяти- и т.д. кратное отражение. Ввиду малой интенсивности лучи трехкратного отражения и выше принимать в расчет не будем (при n1.5 от поверхности пластинки отражается примерно 4%падающего светового потока). Однократно отраженные от пластинки лучи1и2когерентны, если оптическая разность их хода меньше длины когерентности падающей волны. Если на пути лучей поставить собирающую линзу, то на экране, совмещенном с фокальной плоскостью линзы, возникнет интерференционная картина. Роль линзы может играть хрусталик, а экрана – сетчатка глаза. В этом случае глаз должен быть аккомодирован (наведен на резкость) на бесконечность.
Оптическая разность хода, возникающая между двумя интерферирующими лучами от точки Oдо точкиP
. Согласно рис.,. Учитывая закон преломления, получим
.
При вычислении разности колебаний в лучах 1и2нужно, кроме оптической разности хода, учесть возможность изменения фазы волны при отражении. В точкеOотражение происходит от оптически более плотной среды. Поэтому фаза отраженной волны изменяется на(для определенности считаем, что происходит потеря полуволны). В точкеCотражение происходит от оптически менее плотной среды, так что скачка фазы не происходит. С учетом потери полуволны для оптической разности хода получим
. (1)
В точке Pбудет интерференционный максимум, если
, (2а) и минимум, если
. (2б) Выясним условия, при которых эти волны окажутся когерентными и смогут интерферировать. Для того, чтобы имела место временная когерентность, разность хода (1) не должна превышать длину когерентности. Следовательно, должно выполнятся условие
. В данном соотношении, поэтому условию временной когерентности можно придать вид
. (3) Положив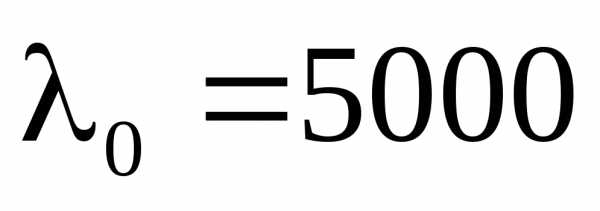 Å и
Å и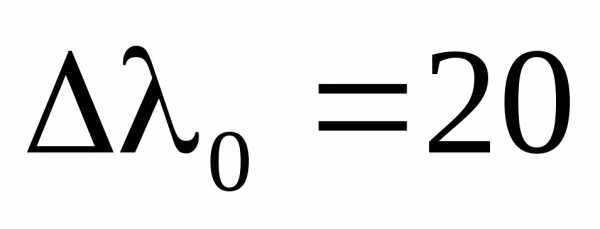 Å, получим предельное значение толщины пластинки – 0,06 мм. Пусть пластинка освещается рассеянным монохроматическим светом (рис.). В рассеянном свете имеются лучи самых разнообразных направлений. Лучи, параллельные некоторому направлению, после отражения соберутся в одной точке и создадут в ней освещенность, определяемую значением оптической разности хода. Лучи, идущие в другом направлении, соберутся в другой точке и т.д. В результате возникает система чередующихся светлых и темных полос (если линза параллельна пластинке, полосы имеет вид концентрических колец с центром в фокусе линзы). Каждая полоса образована лучами, падающими на пластинку под одинаковым углом. Поэтому получающиеся интерференционные полосы носят названиеполос равного наклона.
Å, получим предельное значение толщины пластинки – 0,06 мм. Пусть пластинка освещается рассеянным монохроматическим светом (рис.). В рассеянном свете имеются лучи самых разнообразных направлений. Лучи, параллельные некоторому направлению, после отражения соберутся в одной точке и создадут в ней освещенность, определяемую значением оптической разности хода. Лучи, идущие в другом направлении, соберутся в другой точке и т.д. В результате возникает система чередующихся светлых и темных полос (если линза параллельна пластинке, полосы имеет вид концентрических колец с центром в фокусе линзы). Каждая полоса образована лучами, падающими на пластинку под одинаковым углом. Поэтому получающиеся интерференционные полосы носят названиеполос равного наклона.
Согласно формуле (2а) положение максимумов зависит от длины волны 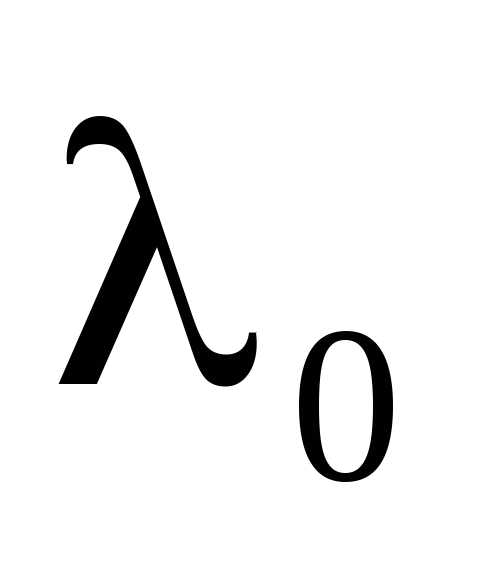 . Поэтому в белом свете интерференционная картина приобретает радужную окраску. Возможность наблюдения интерференционной картины в белом свете определяется способностью глаза различать оттенки цвета. Средний глаз отличает цвета, отличающиеся по длине волны не менее чем на 20 Å. Именно такое значение
. Поэтому в белом свете интерференционная картина приобретает радужную окраску. Возможность наблюдения интерференционной картины в белом свете определяется способностью глаза различать оттенки цвета. Средний глаз отличает цвета, отличающиеся по длине волны не менее чем на 20 Å. Именно такое значение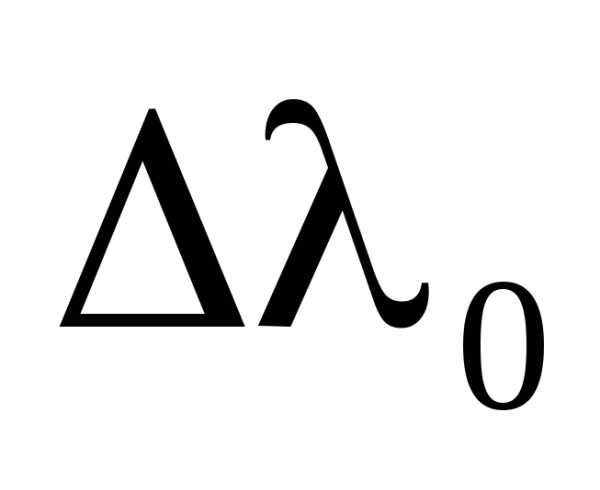 взято при оценке толщины пластинки.
взято при оценке толщины пластинки.
Пластинка переменной толщины.Пусть на клин с острым углом (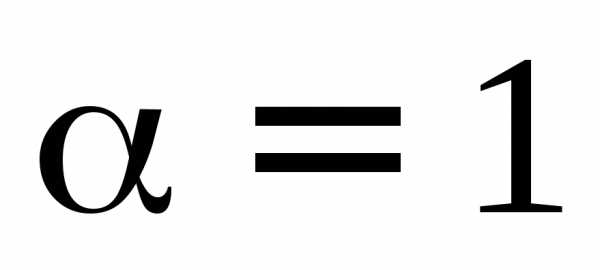 ) падает плоская световая волна. При отражении падающего луча1от верхней и нижней поверхностей клина возникают лучи1 и1соответственно. При распространении они пересекаются в точке
) падает плоская световая волна. При отражении падающего луча1от верхней и нижней поверхностей клина возникают лучи1 и1соответственно. При распространении они пересекаются в точке . Можно показать, что аналогичные точки пересечения других пар отраженных лучей лежат в одной плоскости, проходящей через вершину клинаO. Временная когерентность будет выполняться для тех лучей, для которых толщина клина в месте отражения удовлетворяет условию (3). Допустим, что это условие выполняется для всего клина или хотя бы для его части. Тогда в плоскости экрана
. Можно показать, что аналогичные точки пересечения других пар отраженных лучей лежат в одной плоскости, проходящей через вершину клинаO. Временная когерентность будет выполняться для тех лучей, для которых толщина клина в месте отражения удовлетворяет условию (3). Допустим, что это условие выполняется для всего клина или хотя бы для его части. Тогда в плоскости экрана будет наблюдаться интерференционная картина в виде полос, параллельных ребру клинаO. Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, вследствие чего их называютполосами равной толщины.
будет наблюдаться интерференционная картина в виде полос, параллельных ребру клинаO. Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, вследствие чего их называютполосами равной толщины.
При другом расположении экрана (например,  и
и ) интерференция также возможна. Поскольку, в этом случае на экране пересекаются отражения разных лучей, то соответствующие падающие лучи должны быть пространственно когерентны (например, когерентны лучи1и2– экран
) интерференция также возможна. Поскольку, в этом случае на экране пересекаются отражения разных лучей, то соответствующие падающие лучи должны быть пространственно когерентны (например, когерентны лучи1и2– экран или1и3– экран
или1и3– экран ). При ограниченной пространственной когерентности область локализации интерференционной картины (т.е. область пространства, располагая в которой экран можно наблюдать на нем интерференционную картину) также оказывается ограниченной. Причем эта область тем уже, чем меньше степень пространственной когерентности падающей волны.
). При ограниченной пространственной когерентности область локализации интерференционной картины (т.е. область пространства, располагая в которой экран можно наблюдать на нем интерференционную картину) также оказывается ограниченной. Причем эта область тем уже, чем меньше степень пространственной когерентности падающей волны.
Рассмотрим условия соблюдения пространственной когерентности. При рассмотрении считаем толщину пластинки неизменной. Из рис. видно, что расстояние между падающими лучами 1и2равно
. Если принять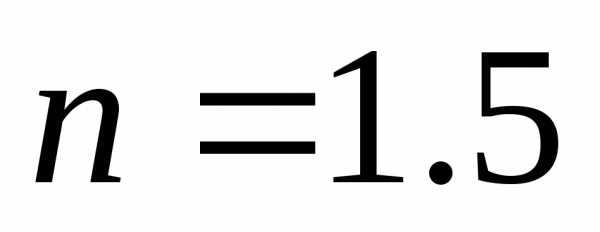 , то для
, то для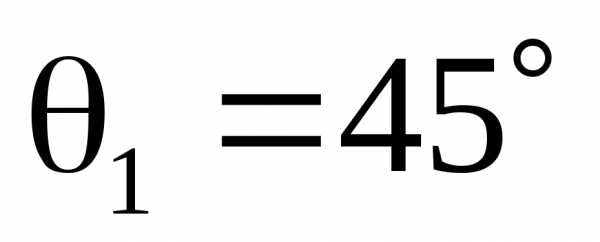 получается(для нормального падения
получается(для нормального падения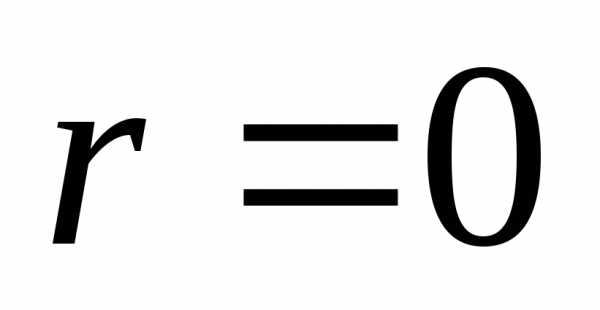 ). Радиус когерентности солнечного света имеет значение порядка 0,05 мм. Следовательно, для возникновения интерференции в этих условиях должно выполнятьсяd 0.05 мм. Таким образом, требования временной и пространственной когерентности дают близкие значения толщины пластинки, при которой в солнечном свете будет наблюдаться интерференция. При освещении светом с большей степенью когерентности интерференция наблюдается и при отражении от более толстых пластинок или пленок.
). Радиус когерентности солнечного света имеет значение порядка 0,05 мм. Следовательно, для возникновения интерференции в этих условиях должно выполнятьсяd 0.05 мм. Таким образом, требования временной и пространственной когерентности дают близкие значения толщины пластинки, при которой в солнечном свете будет наблюдаться интерференция. При освещении светом с большей степенью когерентности интерференция наблюдается и при отражении от более толстых пластинок или пленок.
Практически полосы равной толщины наблюдают визуально либо поместив линзу и за ней экран. При наблюдении в белом свете полосы будут окрашенными, так что поверхность пластинки или пленки будет представляться окрашенной. Такую окраску имеют, например, расплывшиеся на поверхности воды тонкие пленки нефти или масла, а также мыльные пленки. Цвета побежалости, возникающие на поверхности стальных изделий при их закалке, также обусловлены интерференцией от пленки прозрачных окислов.
Сопоставим два рассмотренных случая интерференции при отражении от тонких пленок. Полосы равного наклона получаются при освещении пластинки постоянной толщины () рассеянным светом, в котором содержатся лучи разных направлений. Локализованы полосы равного наклона в бесконечности. Полосы равной толщины наблюдаются при освещении пластинки непостоянной толщины параллельным пучком света (). Локализованы полосы раной толщины вблизи пластинки. В реальных условиях изменяется как угол падения лучей, так и толщина пленки. В этом случае наблюдается полосы смешанного типа.
Кольца Ньютона.Классическим примером полос равной толщины являютсякольца Ньютона. Они наблюдаются при отражении света от соприкасающихся друг с другом толстой плоскопараллельной стеклянной пластинки и плоско-выпуклой линзы с большим радиусом кривизны (рис). Роль тонкой пленки, от поверхностей которой отражаются когерентные волны, играет воздушный зазор между пластинками и линзой (вследствие большой толщины пластинки и линзы, отраженные от других поверхностей лучи в образовании интерференционной картины не участвуют). При нормальном падении света полосы равной толщины имеют вид концентрических окружностей, при наклонном падении – эллипсов. Найдем радиусы колец Ньютона, получающихся при падении света по нормали к пластинке. Из рис. следует, что
, гдеR– радиус кривизны линзы,r– радиус окружности, которой соответствует зазор толщиныd. Таким образом,
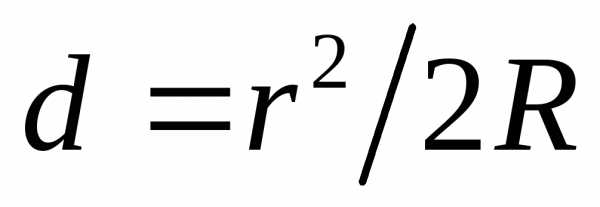 . С учетом потери полуволны, возникающей при отражении от пластинки, оптическая разность хода лучей1и1равна
. С учетом потери полуволны, возникающей при отражении от пластинки, оптическая разность хода лучей1и1равна
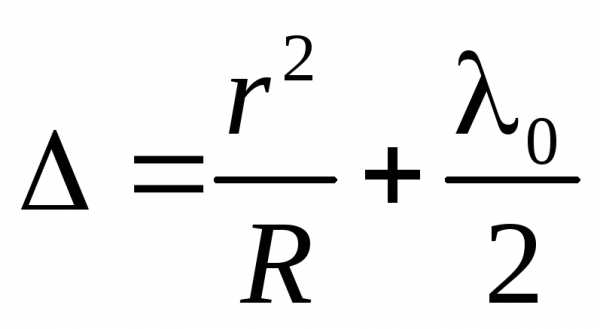 .
.
Используя условия максимума (2а) и минимума (2б), получим выражения для радиусов m-го светлого иm-го темного кольца соответственно
, (4а). (4б)
Многолучевая интерференция.До сих пор рассматривалась двухлучевая интерференция. Теперь исследуем случай, когда интерферируют много световых лучей.
Допустим, что в данную точку экрана приходит Nлучей одинаковой интенсивности, причем фаза каждого следующего луча сдвинута относительного фазы предыдущего на одну и ту же величину. Представим световые колебания в комплексной форме с помощью рекуррентного соотношения
. Результирующее колебание определяется суммой геометрической прогрессии
. Расчет интенсивности, возникающей при интерференции, дает значение
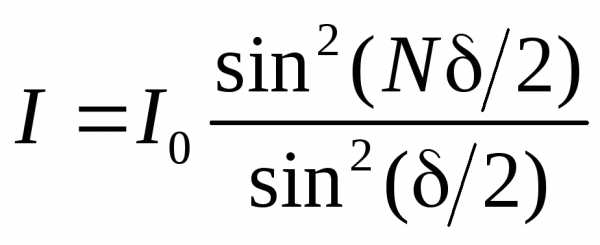 , (5) где
, (5) где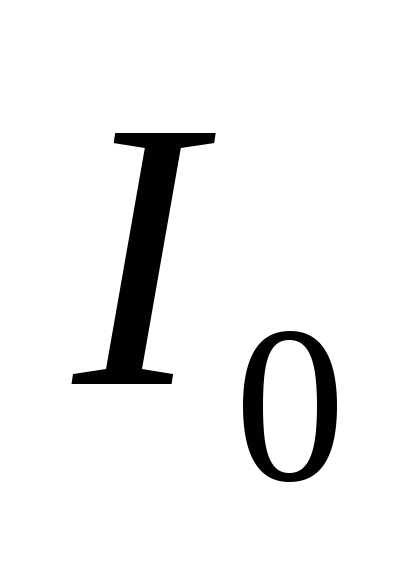 – интенсивность, создаваемая каждым лучом в отдельности.
– интенсивность, создаваемая каждым лучом в отдельности.
При значениях () результирующая интенсивность оказывается равной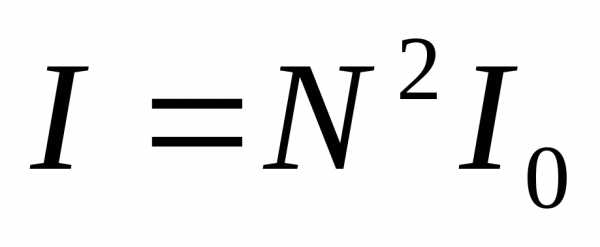 , что соответствуетглавным максимумам. Числоmназываетсяпорядкомглавного максимума. В промежутке между главными максимумами располагается
, что соответствуетглавным максимумам. Числоmназываетсяпорядкомглавного максимума. В промежутке между главными максимумами располагается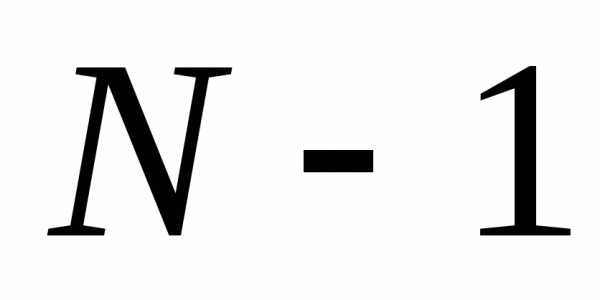 минимум интенсивности. В свою очередь между
минимум интенсивности. В свою очередь между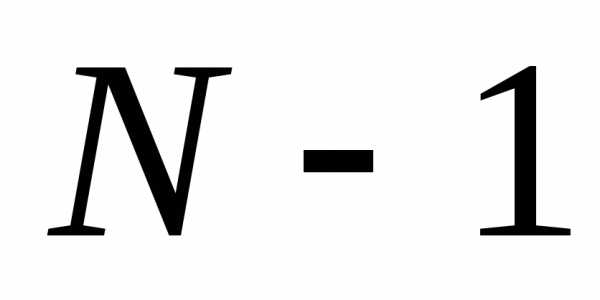 минимумами располагается
минимумами располагается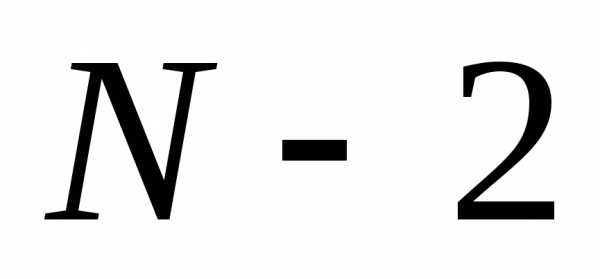 вторичных максимумов. Наибольшей интенсивностью обладают вторичные максимумы, ближайшие к главным максимумам. При большомNони имеют интенсивность в22 раза меньшую, чем интенсивность главного максимума. Ситуация близкая к многолучевой интерференции возникает в дифракционной решетке, которая будет рассмотрена позднее.
вторичных максимумов. Наибольшей интенсивностью обладают вторичные максимумы, ближайшие к главным максимумам. При большомNони имеют интенсивность в22 раза меньшую, чем интенсивность главного максимума. Ситуация близкая к многолучевой интерференции возникает в дифракционной решетке, которая будет рассмотрена позднее.
Теперь рассмотрим интерференцию очень большого числа лучей (), интенсивность которых убывает в геометрической прогрессии. Предположим, что колебания имеют вид
, где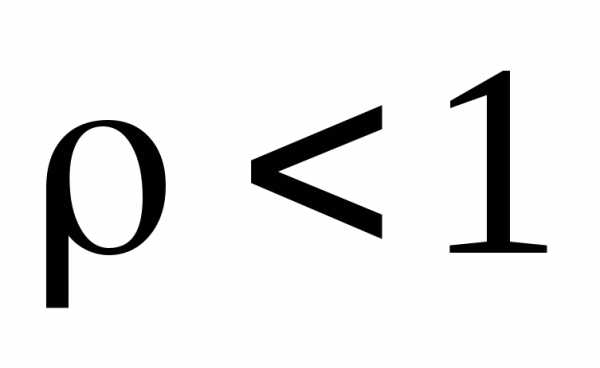 – постоянная величина. Результирующее колебание описывается суммой геометрической прогрессии
– постоянная величина. Результирующее колебание описывается суммой геометрической прогрессии
с интенсивностью равной
, (6) где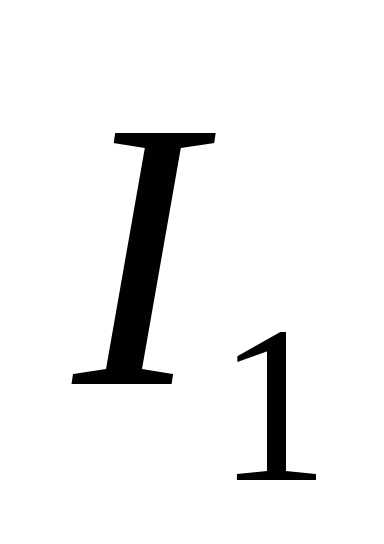 – интенсивность первого (наиболее интенсивного) луча.
– интенсивность первого (наиболее интенсивного) луча.
При значениях () выражение (6) имеет максимумы
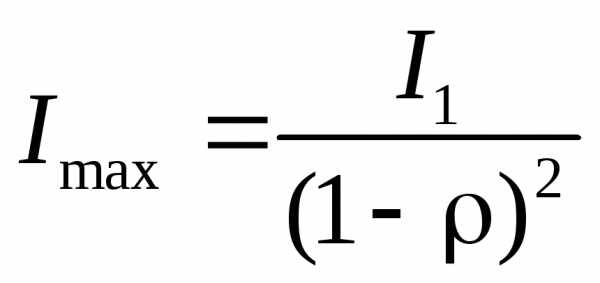 . В промежутках между максимумами функция изменяется монотонно, достигая в середине промежутка минимальное значение
. В промежутках между максимумами функция изменяется монотонно, достигая в середине промежутка минимальное значение
. Таким образом,
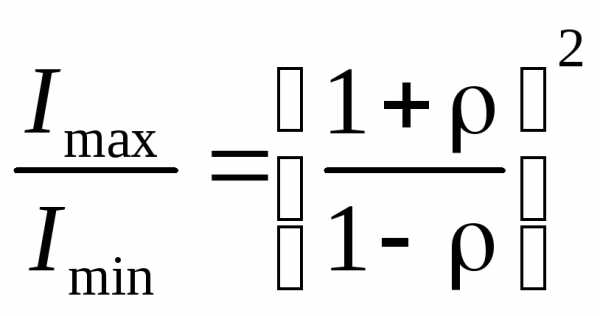 . Интерференционная картина имеет вид узких резких линий на практически темном фоне. Практически случай большого числа лучей с убывающей интенсивностью осуществляется в интерферометреФабри-Перо.
. Интерференционная картина имеет вид узких резких линий на практически темном фоне. Практически случай большого числа лучей с убывающей интенсивностью осуществляется в интерферометреФабри-Перо.
Применение интерференции света.
Просветление оптики. Явление интерференции применяется для улучшения качества оптических приборов и получения высокоотражающих покрытий. Прохождение света через каждую преломляющую поверхность линзы сопровождается отражением4%падающего потока (при показателе преломления стекла1,5). Так как современные объективы состоят из большого количества линз, то число отражений в них велико, а поэтому велики и потери светового потока. Для устранения этого и других недостатков осуществляют так называемоепросветление оптики. Для этого на свободные поверхности линз наносят тонкие пленки с показателем преломления, меньшим, чем у материала линзы. При отражении света от границ раздела воздух–пленка и пленка–стекло возникает интерференция отраженных лучей. Толщину пленкиdи показатели преломления стекла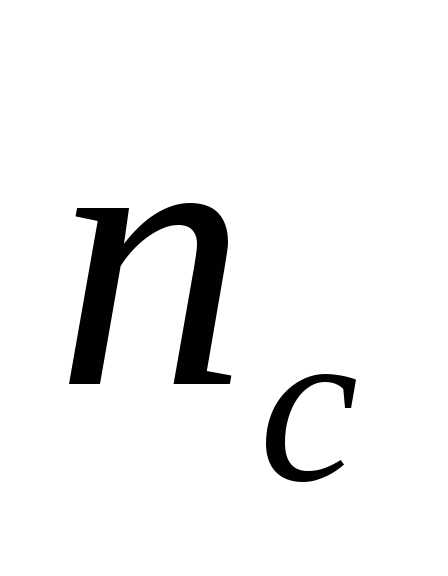 и пленкиnподбираются так, чтобы отраженные волны гасили друг друга. Для этого их амплитуды должны быть равны, а оптическая разность хода равна. Расчет показывает, что амплитуды отраженных лучей равны, если
и пленкиnподбираются так, чтобы отраженные волны гасили друг друга. Для этого их амплитуды должны быть равны, а оптическая разность хода равна. Расчет показывает, что амплитуды отраженных лучей равны, если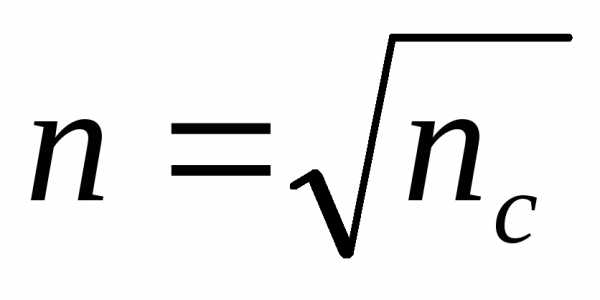 . Так как
. Так как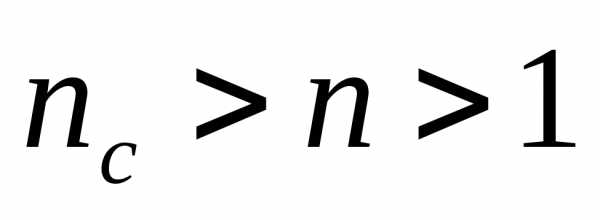 , то потеря полуволны происходит на обеих поверхностях; следовательно, условие минимума (свет падает нормально)
, то потеря полуволны происходит на обеих поверхностях; следовательно, условие минимума (свет падает нормально)
. Обычно принимают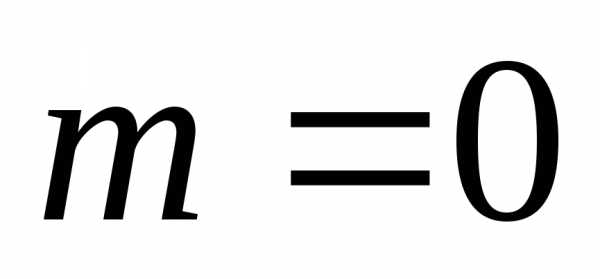 , тогда
, тогда
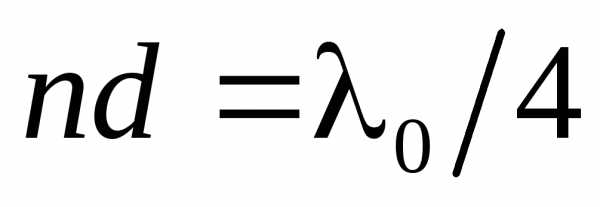 . Так как добиться одновременного гашения для всех длин волн невозможно (показатель преломления зависит от длины волны), то это делается для цвета с(к нему наиболее чувствителен глаз). Поэтому объективы с просветленной оптикой имеют синевато-красный оттенок.
. Так как добиться одновременного гашения для всех длин волн невозможно (показатель преломления зависит от длины волны), то это делается для цвета с(к нему наиболее чувствителен глаз). Поэтому объективы с просветленной оптикой имеют синевато-красный оттенок.
Интерференционные светофильтры.Многолучевую интерференцию можно осуществить в многослойной системе чередующихся пленок с разными показателями преломления (но одинаковой оптической толщиной, равной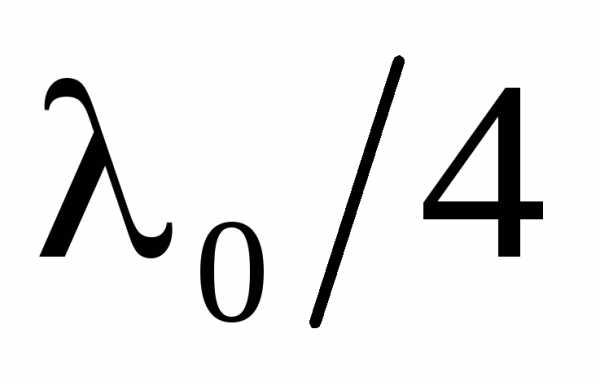 ). При прохождении света возникает большое число отраженных интерферирующих лучей, которые при оптической толщине пленок
). При прохождении света возникает большое число отраженных интерферирующих лучей, которые при оптической толщине пленок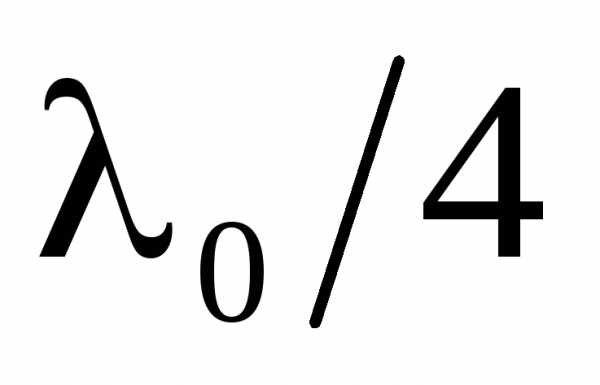 будут взаимно усиливаться, т.е. коэффициент отражения возрастает. Подобные отражатели применяются в лазерной технике, а также используются для создания интерференционных светофильтров.
будут взаимно усиливаться, т.е. коэффициент отражения возрастает. Подобные отражатели применяются в лазерной технике, а также используются для создания интерференционных светофильтров.
Интерферометры.Явление интерференции применяется в очень точных измерительных приборах –интерферометрах. На рис. изображена схемаинтерферометра Майкельсона. Пучок света от источникаSпадает на пластинку , покрытую тонким слоем серебра (благодаря чему коэффициент отражения близок к 0,5). Дальнейший ход интерферирующих лучей ясен из рисунка. На пути луча1ставится точно такая, как
, покрытую тонким слоем серебра (благодаря чему коэффициент отражения близок к 0,5). Дальнейший ход интерферирующих лучей ясен из рисунка. На пути луча1ставится точно такая, как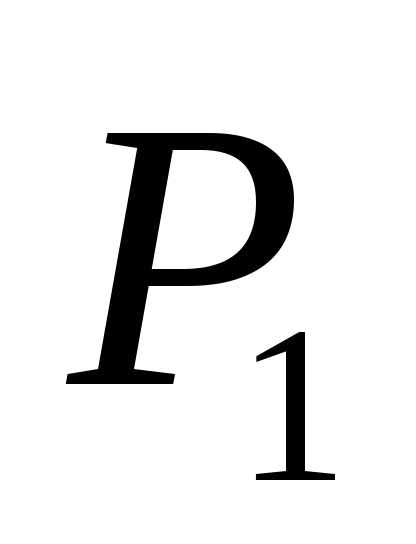 , но не посеребренная пластинка
, но не посеребренная пластинка . Она уравнивает пути лучей1и2в стекле. Интерференционная картина наблюдается с помощью зрительной трубы.
. Она уравнивает пути лучей1и2в стекле. Интерференционная картина наблюдается с помощью зрительной трубы.
Интерференционная картина соответствует интерференции в воздушном слое, образованным зеркалом 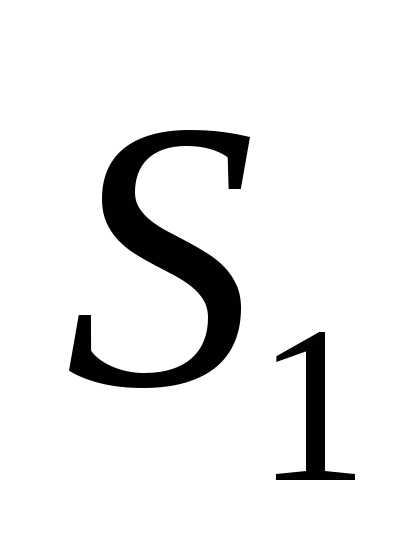 и мнимым изображением
и мнимым изображением зеркала
зеркала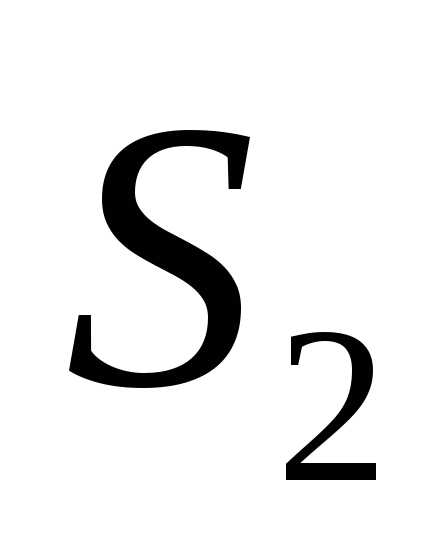 в полупрозрачной пластинке
в полупрозрачной пластинке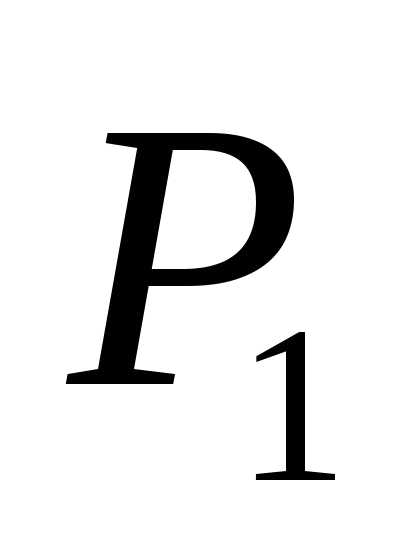 . Характер интерференционной картины зависит от положения зеркал и от расходимости пучка света, падающего на прибор. Если пучок параллелен, а плоскости
. Характер интерференционной картины зависит от положения зеркал и от расходимости пучка света, падающего на прибор. Если пучок параллелен, а плоскости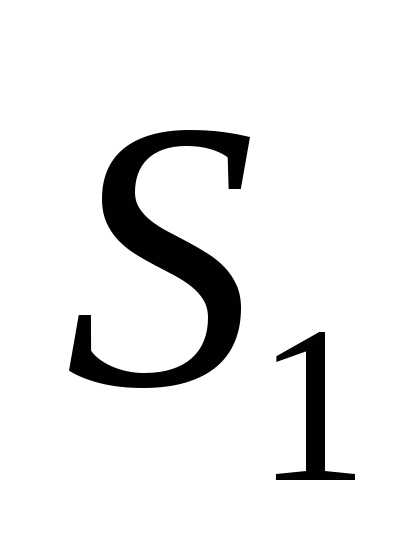 и
и образуют клин, то наблюдается интерференционные полосы равной толщины, расположенные параллельно ребру воздушного клина. При расходящемся пучке света и параллельном расположении плоскостей
образуют клин, то наблюдается интерференционные полосы равной толщины, расположенные параллельно ребру воздушного клина. При расходящемся пучке света и параллельном расположении плоскостей и
и получаются полосы равного наклона, имеющие вид концентрических колец.
получаются полосы равного наклона, имеющие вид концентрических колец.
Интерферометр Фабри-Перосостоит из двух параллельных стеклянных или кварцевых пластинок, разделенных воздушным промежутком (рис.). Интенсивности вышедших из прибора лучей относятся как
Соответственно отношения амплитуд будут следующими
Фаза колебания с увеличением номера луча изменяется на одну и ту же величину, определяющейся оптической разностью хода соседних лучей.
При пропускании сквозь прибор расходящегося пучка света в фокальной плоскости линзы возникают полосы равного наклона, имеющие вид концентрических колец.
Применение интерферометров весьма многообразно. Они применяются для точного (порядка 107м) измерения длин, измерения углов, определения качества оптических деталей, исследования быстропротекающих процессов и др.
studfiles.net
Интерференция в тонких пленках.
Пластинка постоянной толщины. При падении световой волны на тонкую прозрачную пластинку (или пленку) происходит отражение от обеих поверхностей пластинки. В результате возникают две световые волны, которые при определенных условиях могут интерферировать.
Пусть на прозрачную плоскопараллельную пластинку падает плоская световая волна (параллельный пучок света) (рис.17.4). В результате отражений от поверхностей пластинки, часть света возвращается в исходную среду.
В любую точку P, находящуюся с той же стороны от пластинки, что и источник, приходят два луча. Эти лучи образуют интерференционную картину.
Для определения вида полос можно представить себе, что лучи выходят из мнимых изображений S1 и S2 источника S, создаваемых поверхностями пластинки. На удаленном экране, расположенном параллельно пластинке, интерференционные полосы имеют вид концентрических колец с центрами на перпендикуляре к пластинке, проходящем через источник S. Этот опыт предъявляет менее жесткие требования к размерам источника S, чем рассмотренные выше опыты. Поэтому можно в качестве S применить ртутную лампу без вспомогательного экрана с малым отверстием, что обеспечивает значительный световой поток. С помощью листочка слюды (толщиной 0,03 – 0,05 мм) можно получить яркую интерференционную картину прямо на потолке и на стенах аудитории. Чем тоньше пластинка, тем крупнее масштаб интерференционной картины, т.е. больше расстояние между полосами.
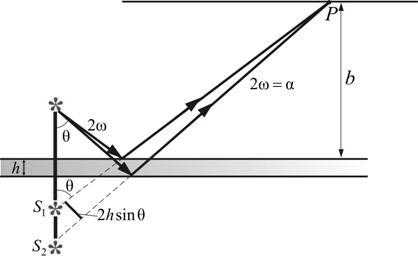
Рис. 17.4
Полосы равного наклона.Особенно важен частный случай интерференции света, отраженного двумя поверхностями плоскопараллельной пластинки, когда точка наблюдения P находится в бесконечности, т.е. наблюдение ведется либо глазом, аккомодированным на бесконечность, либо на экране, расположенном в фокальной плоскости собирающей линзы (рис. 17.5).
В этом случае оба луча, идущие от S к P, порождены одним падающим лучом и после отражения от передней и задней поверхностей пластинки параллельны друг другу. Оптическая разность хода между ними в точке P такая же, как на линии DC:
.
Здесь n – показатель преломления материала пластинки. Предполагается, что над пластинкой находится воздух, т.е. . Так как , (h – толщина пластинки, и – углы падения и преломления на верхней грани; ), то для разности хода получаем
.
Следует также учесть, что при отражении волны от верхней поверхности пластинки в соответствии с формулами Френеля ее фаза изменяется на π. Поэтому разность фаз δ складываемых волн в точке P равна:
,
где – длина волны в вакууме.
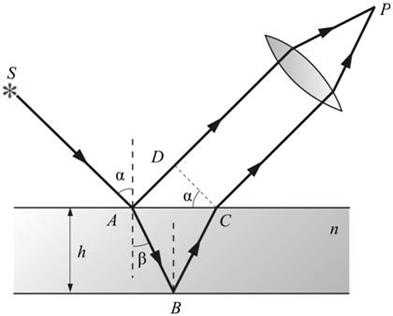
Рис.17.5
В соответствии с последней формулой светлые полосы расположены в местах, для которых , где m – порядок интерференции. Полоса, соответствующая данному порядку интерференции, обусловлена светом, падающим на пластинку под вполне определенным углом α. Поэтому такие полосы называют интерференционными полосами равного наклона. Если ось объектива расположена перпендикулярно пластинке, полосы имеют вид концентрических колец с центром в фокусе, причем в центре картины порядок интерференции максимален.
Полосы равного наклона можно получить не только в отраженном свете, но и в свете, прошедшем сквозь пластинку. В этом случае один из лучей проходит прямо, а другой – после двух отражений на внутренней стороне пластинки. Однако видимость полос при этом низкая.
Для наблюдения полос равного наклона вместо плоскопараллельной пластинки удобно использовать интерферометр Майкельсона (рис.17.6). Рассмотрим схему интерферометра Майкельсона: з1 и з2 – зеркала. Полупрозрачное зеркало посеребрено и делит луч на две части – луч 1 и 2. Луч 1, отражаясь от з1 и проходя , дает , а луч 2, отражаясь от з2 и далее от , дает . Пластинки и одинаковы по размерам. ставится для компенсации разности хода второго луча. Лучи и когерентны и интерферируют.
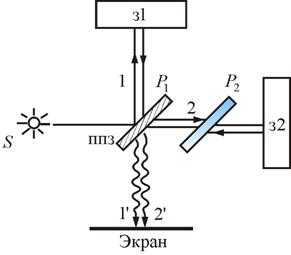
Рис. 17.6
Полосы равной толщины (интерференция от клина). Мы рассмотрели интерференционные опыты, в которых деление амплитуды световой волны от источника происходило в результате частичного отражения на поверхностях плоскопараллельной пластинки. Локализованные полосы при протяженном источнике можно наблюдать и в других условиях. Оказывается, что для достаточно тонкой пластинки или пленки (поверхности которой не обязательно должны быть параллельными и вообще плоскими) можно наблюдать интерференционную картину, локализованную вблизи отражающей поверхности. Возникающие при этих условиях полосы называют полосами равной толщины. В белом свете интерференционные полосы окрашены. Поэтому такое явление называют цветами тонких пленок. Его легко наблюдать на мыльных пузырях, на тонких пленках масла или бензина, плавающих на поверхности воды, на пленках окислов, возникающих на поверхности металлов при закалке, и т.п.
Рассмотрим интерференционную картину, получаемую от пластинок переменной толщины (от клина).
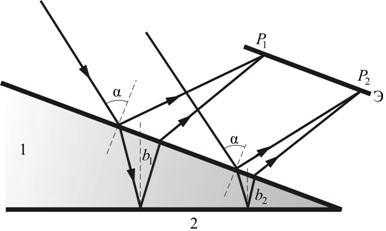
Рис. 17.7
Направления распространения световой волны, отраженной от верхней и нижней границы клина, не совпадают (рис.17.7). Отраженные и преломленные лучи встречаются, поэтому интерференционную картину при отражении от клина можно наблюдать и без использования линзы, если поместить экран в плоскость точек пересечения лучей (хрусталик глаза помещают в нужную плоскость).
Интерференция будет наблюдаться только во 2-й области клина, так как в 1-й области оптическая разность хода будет больше длины когерентности.
Результат интерференции в точках и экрана определяется по известной формуле , подставляя в неё толщину пленки в месте падения луча ( или ). Свет обязательно должен быть параллельным ( ): если одновременно будут изменяться два параметра b и α, то устойчивой интерференционной картины не будет.
Рис.17.8
Поскольку разность хода лучей, отразившихся от различных участков клина, будет неодинаковой, освещенность экрана будет неравномерной, на экране будут темные и светлые полосы (или цветные при освещении белым светом, как показано на рис.17.8). Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, поэтому их называют полосами равной толщины.
Кольца Ньютона.На рис.17.9 изображена оправа, в которой зажаты две стеклянные пластины. Одна из них слегка выпуклая, так что пластины касаются друг друга в какой-то точке. И в этой точке наблюдается нечто странное: вокруг нее возникают кольца. В центре они почти не окрашены, чуть дальше переливаются всеми цветами радуги, а к краю теряют насыщенность цветов, блекнут и исчезают.
Так выглядит эксперимент, в XVII веке положивший начало современной оптике. Ньютон подробно исследовал это явление, обнаружил закономерности в расположении и окраске колец, а также объяснил их на основе корпускулярной теории света.
Кольцевые полосы равной толщины, наблюдаемые в воздушном зазоре между соприкасающимися выпуклой сферической поверхностью линзы малой кривизны и плоской поверхностью стекла называют кольцами Ньютона.
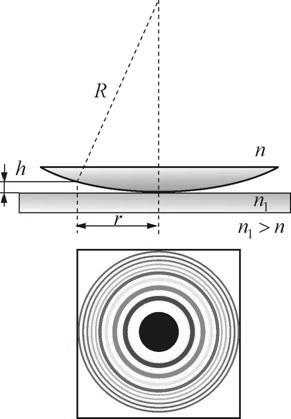 Рис. 17.9
Рис. 17.9
|
Общий центр колец расположен в точке касания. В отраженном свете центр темный, так как при толщине воздушной прослойки, на много меньшей, чем длина волны , разность фаз интерферирующих волн обусловлена различием в условиях отражения на двух поверхностях и близка к π. Толщина h воздушного зазора связана с расстоянием r до точки касания:
.
Здесь использовано условие . При наблюдении по нормали темные полосы, как уже отмечалось, соответствуют толщине , поэтому для радиуса m-го темного кольца получаем
(m = 0, 1, 2, …).
Если линзу постепенно отодвигать от поверхности стекла, то интерференционные кольца будут стягиваться к центру. При увеличении расстояния на картина принимает прежний вид, так как место каждого кольца будет занято кольцом следующего порядка. С помощью колец Ньютона, как и в опыте Юнга, можно сравнительно простыми средствами приближенно определить длину волны света.
Итак, полосы равного наклона получаются при освещении пластинки постоянной толщины рассеянным светом, в котором содержатся лучи разных направлений. Полосы равной толщины наблюдаются при освещении пластинки переменной толщины (клина) параллельным пучком света. Полосы равной толщины локализованы вблизи пластинки.
Просветление оптики
Одной из важных задач, возникающих при построении различных оптических и антенных устройств СВЧ-диапазона, является уменьшение потерь ( ) интенсивности света, мощности потока электромагнитной энергии при отражении от поверхностей линз, обтекателей антенн и пр. приборов, используемых для преобразований световых и радиоволн в разнообразных приборах фотоники, оптоэлектроники и радиоэлектроники. Для уменьшения потерь на отражение используется покрытие оптических деталей (линз) 3 пленкой 2 со специальным образом подобранными толщиной δ и показателем преломления n (рис. 17.10).
Идея уменьшения интенсивности отраженного света от поверхности оптических деталей состоит в интерференционном гашении волны, отраженной от внешней поверхности детали 1, волной отражённой от внутренней 2. Для осуществления этого амплитуды обеих волн должны быть равны, а фазы отличаться на 180°. В этом случае обеспечивается гашение отражённой волны. Необходимое соотношение между фазами отражённых волн обеспечивается выбором толщины плёнки δ, кратной нечётному числу четвертей длины волны проходящего через рассматриваемую деталь света: .
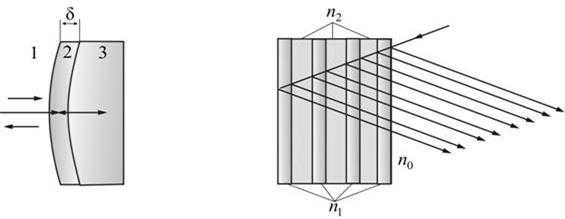
Рис. 17.10
Таким образом, если выполняется данное условие, то в результате интерференции наблюдается гашение отраженных лучей.
Так как добиться одновременного гашения для всех длин волн невозможно, то его делают для . Поэтому объективы с просветленной оптикой кажутся голубыми.
infopedia.su