Интерференция света при отражении от тонких пластинок. Интерференция света при отражении от тонких пленок
30) Интерференция при отражении от тонких плёнок
Луч света, падающий на прозрачную пластинку, частично отражается и частично преломляется. Преломленный луч, отражаясь от нижней поверхности пластинки, идет к верхней и преломляется на ней второй раз. Таким образом получаются два луча.
Если источник света естественный, то необходимым условием когерентности является малая толщина пластинок (интерференция в тонких пленках). При освещении лазерным лучом это ограничение отпадает.
При определении оптической разности хода необходимо учитывать изменение фазы отраженной волны на противоположную, если отражение происходит от оптически более плотной среды.
Для n1 = 1 и n3 > n2 оптическая разность хода Δ = n2S2 - S1. После преобразований с учетом закона преломления и тригонометрических формул получим:
Если n3 < n2, тогда: Здесь λ0/2 появилась за счет изменения фазы волны на противоположную при отражении в точке A.
31) Кольца Ньютона
Плосковыпуклая линза большого радиуса кладется на стеклянную пластинку и освещается сверху параллельным пучком света. Так как радиус линзы R велик по сравнению с r - радиусом интерференционных полос, то угол падения света на внутреннюю поверхность линзы i ≈ 0. Тогда геометрическая разность хода с большой точностью равна 2b. При нахождении оптической разности хода следует учитывать изменение фазы на противоположную при отражении от оптически более плотной среды. Связь между b, r и R нетрудно найти из геометрических соображений. 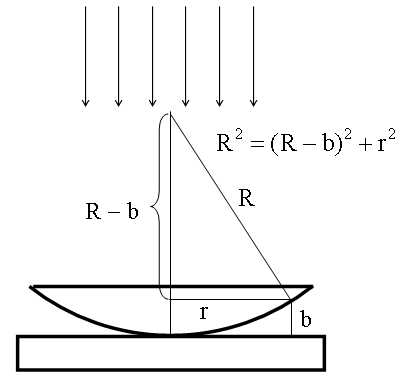
max
min
32) Дифракция света. Принцип Гюйгенса-Френеля
Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий.
>Принцип Гюйгенса-Френеля
Каждая точка поверхности, достигнутая световой волной, является вторичным источником сферических световых волн. Огибающая вторичных волн становится фронтом волны в следующий момент времени.
33) Зоны Френеля
Френель предложил оригинальный метод разбиения волновой поверхности S на зоны, позволивший сильно упростить решение задач (метод зон Френеля).
Границей первой (центральной) зоны служат точки поверхности S, находящиеся на расстоянии от точки M (рис. 9.2). Точки сферы S, находящиеся на расстояниях,, и т.д. от точки M, образуют 2, 3 и т.д. зоны Френеля.
Колебания, возбуждаемые в точке M между двумя соседними зонами, противоположны по фазе, так как разность хода от этих зон до точки M .
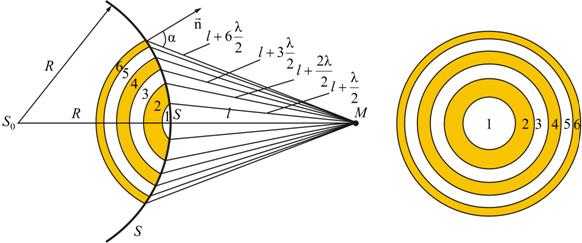
Рис. 9.2
Поэтому при сложении этих колебаний, они должны взаимно ослаблять друг друга: , где A – амплитуда результирующего колебания, – амплитуда колебаний, возбуждаемая i-й зоной Френеля.
Величина зависит от площадизоны и угламежду нормалью к поверхности и прямой, направленной в точкуM.
Площадь одной зоны .
Отсюда видно, что площадь зоны Френеля не зависит от номера зоны i. Это значит, что при не слишком больших i площади соседних зон одинаковы.
В то же время с увеличением номера зоны возрастает угол и, следовательно, уменьшается интенсивность излучения зоны в направлении точки M, т.е. уменьшается амплитуда. Она уменьшается также из-за увеличения расстояния до точки M:.
Отсюда следует, что углы между нормалью к зоне и направлением на точку M у соседних зон примерно равны, т.е. что амплитуды волн, приходящих в точку M от соседних зон, примерно равны.
Световая волна распространяется прямолинейно. Фазы колебаний, возбуждаемые соседними зонами, отличаются на π. Поэтому в качестве допустимого приближения можно считать, что амплитуда колебания от некоторойm-й зоны равна среднему арифметическому от амплитуд примыкающих к ней зон, т.е. .
Результирующая амплитуда, создаваемая в некоторой точке M всей сферической поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной , а интенсивность.
studfiles.net
12.Интерференция света при отражении от тонких пластинок. Полосы равной толщины и равного наклона.
Большой практический интерес представляет интерференция в тонких пластинках и пленках.
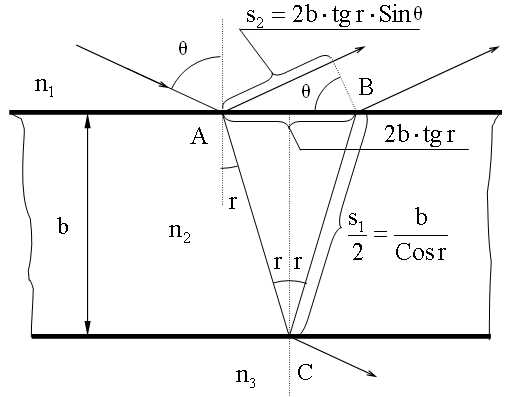
Пусть на тонкую плоскопараллельную пластину толщиной b, изготовленную из прозрачного вещества с показателем преломления n, из воздуха (nвозд » 1) падает плоская световая волна, которую можно рассматривать как параллельный пучок лучей (рис.4), под углом Q1 к перпендикуляру.
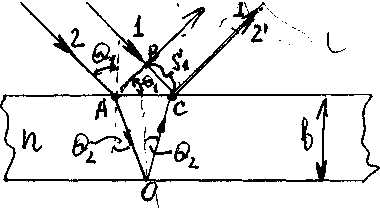
Рис.4.
На поверхности пластины в точке А луч разделится на два параллельных луча света, из которых один образуется за счет отражения от верхней поверхности пластинки, а второй – от нижней поверхности. Разность хода, приобретаемая лучами 1 и 2 до того, как они сойдутся в точке С, равна
D = nS2 – S1 ± l0/2
где S1 - длина отрезка АВ, а S2 – суммарная длина отрезков АО и ОС, а член ± l0/2 обусловлен потерей полуволны при отражении света от границы раздела двух сред с различными показателями преломления (n >nв –точка С) .
Из геометрического рассмотрения получается формула для оптической разности хода дучей1и2:
D' = 2bÖ(n2 – sin2Q1) = 2bn соsQ2,
ас учетом потери полуволны для оптической разности хода получим
D = 2bÖ(n2 – sin2Q1) ± l0/2 = 2bn соsQ2 ± l0/2. (10)
Вследствие ограничений, накладываемых временной и пространственной когерентностью, интерференция при освещении пластинки например солнечным светом наблюдается только в том случае, если толщина пластинки не превышает нескольких сотых миллиметра. При освещении светом с большей степенью когерентности (например, лазером) интерференция, наблюдается и при отражении от более толстых пластинок или пленок.
Практически интерференцию от плоскопараллельной пластинки наблюдают, поставив на пути отраженных пучков линзу, которая собирает лучи в одной из точек экрана, расположенного в фокальной плоскости линзы (рис.5). Освещенность в произвольной точке Р экрана зависит от значения величины D, определенной по формуле (10). При D = mlо получаются максимумы, при D = (m + 1/2)lо - минимумы интенсивности (m - целое число).
Пусть тонкая плоскопараллельная пластинка освещается рассеянным монохроматическим светом (рис.5). Расположим параллельно пластинке линзу, в фокальной плоскости которой поместим экран. В рассеянном свете имеются лучи самых разнообразных направлений. Лучи, параллельные плоскости рисунка и падающие на пластинку под углом Q'1, после отражения от обеих поверхностей пластинки соберутся линзой в точке Р и создадут в этой точке освещенность, определяемую значением оптической разности хода.
E
Рис.5.
Лучи, идущие в других плоскостях, но падающие на пластинку под тем же углом Q1¢ соберутся линзой в других точках, отстоящих от центра экрана О на такое же расстояние, как и точка Р. Освещенность во всех этих точках будет одинакова. Т.о. лучи, падающие на пластинку под одинаковым углом Q1¢, создадут на экране совокупность одинаково освещенных точек, расположенных по окружности с центром в точке О. Аналогично, лучи, падающие под другим углом Q"1 создадут на экране совокупность одинаково (но иначе, поскольку Δ иная) освещенных точек, расположенных по окружности другого радиуса.
В результате на экране возникнет система чередующихся светлых и темных круговых полос с общим центром в точке O). Каждая полоса образована лучами, падающими на пластинку под одинаковым углом Q1. Поэтому получающиеся в описанных условиях интерференционные полосы носят назв. полос равного наклона. При ином расположении линзы относительно пластинки (экран во всех случаях должен совпадать с фокальной плоскостью линзы) форма полос равного наклона будет другой. Роль линзы может играть хрусталик глаза, а экрана - сетчатка глаза.
Согласно (10) положение максимумов зависит от lо. Поэтому в белом свете получается совокупность смещенных др. относительно др. полос, образованных лучами разных цветов, и интерференционная картина приобретает радужную окраску.
Интерференционная картина от тонкого прозрачного клина переменной толщины была изучена еще Ньютоном. Пусть на такой клин (рис.6) падает параллельный пучок лучей.
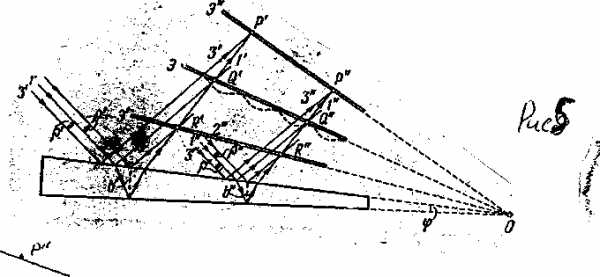
Теперь лучи, отразившиеся от разных поверхностей клина, не будут параллельными. Но и в этом случае отраженные волны будут когерентными во всем пространстве над клином, и при любом расстоянии экрана от клина на нем будет наблюдаться интерференционная картина в виде полос, параллельных вершине клина 0. Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, вследствие чего их называют полосами равной толщины. Практически полосы равной толщины наблюдают, поместив вблизи клина линзу и за ней экран. Роль линзы может играть хрусталик, а роль экрана - сетчатка глаза. При наблюдении в белом свете полосы будут окрашенными, так что поверхность пластинки или пленки представляется имеющей радужную окраску. Такую окраску имеют, например, расплывшиеся по поверхности воды тонкие пленки нефти и масла, а также мыльные пленки. Заметим, что интерференция от тонких пленок может наблюдаться не только в отраженном, но и в проходящем свете.
studfiles.net
Интерференция света при отражении от тонких пластинок
⇐ ПредыдущаяСтр 2 из 2При падении световой волны на тонкую прозрачную пластинку (или пленку) происходит отражение от обеих поверхностей пластинки. В результате возникают две световые волны, которые при известных условиях могут интерферировать.
Пусть на прозрачную плоскопараллельную пластинку падает плоская световая волна, которую можно рассматривать как параллельный пучок лучей (рисунок 1). Пластинка отбрасывает вверх два параллельных пучка света,
Рисунок 1 – Тонкая пластина
из которых один образовался за счет отражения от верхней поверхности пластинки, второй — вследствие отражения от нижней поверхности (на рис. 1 каждый из этих пучков представлен только одним лучом). При входе в пластинку и при выходе из нее второй пучок претерпевает преломление. Кроме этих двух пучков, пластинка отбросит вверх пучки, возникающие в результате трехкратного, пятикратного и т. д. отражения от поверхностей пластинки. Однако ввиду их малой интенсивности мы эти пучки принимать во внимание не будем). Не будем также интересоваться пучками, прошедшими через пластинку.
Разность хода, приобретаемая лучами 1 и 2 до того, как они сойдутся в точке С, равна
(1)
где s1 — длина отрезка ВС, a s2— суммарная длина отрезков АО и ОС, п — показатель преломления пластинки. Показатель преломления среды, окружающей пластинку, полагаем равным единице. Из рис. 1 видно, что
(b — толщина пластинки). Подстановка этих значений в выражение (1) дает
(2)
При вычислении разности фаз между колебаниями в лучах 1 и 2 нужно, кроме оптической разности хода Δ, учесть возможность изменения фазы волны при отражении. В точке С (см. рисунок 1) отражение происходит от границы раздела среды, оптически менее плотной, со средой, оптически более плотной. Поэтому фаза волны претерпевает изменение на π. В точке О отражение происходит от границы раздела среды, оптически более плотной, со средой, оптически менее плотной, так что скачка фазы не происходит. В итоге между лучами 1 и 2 возникает дополнительная разность фаз, равная π. Ее можно учесть, добавив к Δ (или вычтя из нее) половину длины волны в вакууме. В результате получим
(3)
Итак, при падении на пластинку плоской волны образуются две отраженные волны, разность хода которых определяется формулой (3).
Учитывая малость углов и фиксацию радиуса светлых колец интерференуионной картины, можно определить показатель преломления стеклянной пластины по формуле:
(4)
где ; толщина пластины b = 0,02м; = 6,328×10-7 м
Рисунок 2 - Установка
Ход работы
Схема экспериментальной установки представлена на рисунок 2. В ходе проведения работы необходимо измерить расстояние между поверхностью стеклянной пластинки и экраном - l. Закрепив на экране лист бумаги с отверстием для прохождения луча, зарисовать на ней не менее 5 светлых интерференционных колец. Произвести измерения колец и заполнить таблицу.
l = м
Таблица 1
| Величина | m=1 | m=2 | m=3 | m=4 | m=5 | Результат |
| rm | 6,2·10-3 | 9·10-3 | 10,8·10-3 | 12,8·10-3 | 14,7·10-3 | ---- |
| (rm/2l)2 | 4,542·10-5 | 9,56·10-5 | 13,78·10-5 | 19,36·10-5 | 25,5·10-5 | ---- |
| n | 1,436 | 1,512 | 1,452 | 1,53 | 1,614 | <n> = 1,509 |
| δn | -0,073 | 0,003 | -0,057 | 0,018 | 0,105 | <δn> = -0,004 |
| (δn)2 | 5,329·10-3 | 0,009·10-3 | 5,24·10-3 | 0,324·10-3 | 11,025·10-3 | Σ(δn)2= 19,94·10-3 |
t0,955 =2,78
n = 1,5±0,088
⇐ Предыдущая12©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.
arhivinfo.ru