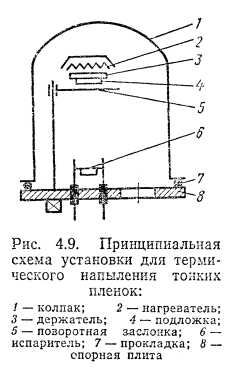
Интерференция света в тонких пленках. Просветление оптики. Дифракция в тонких пленках
Волновая оптика. Интерференция света
Волновая оптика изучает оптические явления, в которых проявляется волновая природа света (интерференция, дифракция, поляризация, дисперсия).
Перераспределение светового потока в пространстве (возникновение максимумов и минимумов интенсивности) при наложении световых волн называется интерференцией. Условием наблюдения интерференции является когерентных волн (волны одной частоты) и постоянной разности фаз δ, 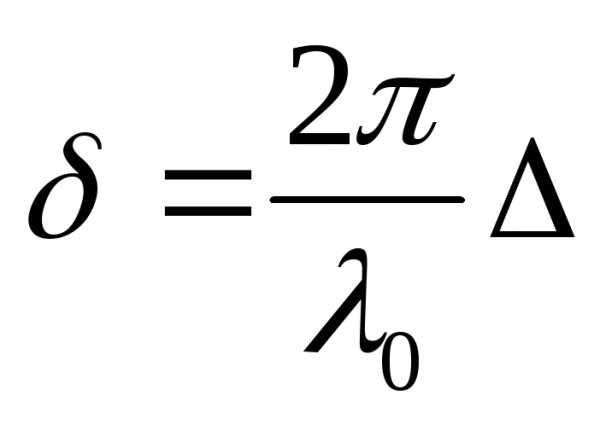 ,
,
где λ0– длина волны в вакууме, Δ – оптическая разность хода двух волн,(рис. 4.6).
Если Δ=±mλ0, то, (m= 0, 1, 2…) и в точке наблюдения (рис.4.6, штрихпунктирные линии, точка наблюдения О) будет максимум интенсивности (условие максимума).
Е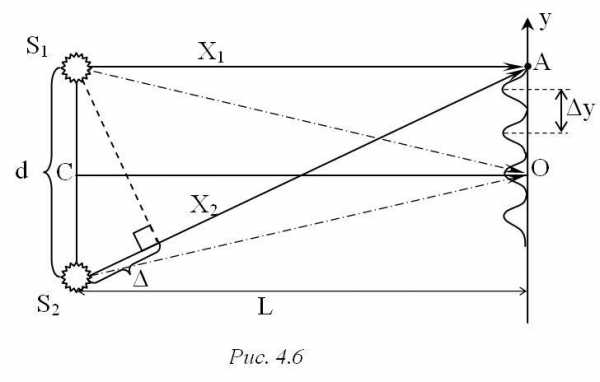 сли Δ=±(m+ ½ )λ0то(m= 0, 1, 2…) и в точке наблюдения будет интерференционный минимум (условие минимума) (рис. 4.6, сплошные линии, точка наблюдения А).
сли Δ=±(m+ ½ )λ0то(m= 0, 1, 2…) и в точке наблюдения будет интерференционный минимум (условие минимума) (рис. 4.6, сплошные линии, точка наблюдения А).
Расстояние между двумя соседними минимумами (или максимумами) называется шириной интерференционной полосы Δх (или Δу): 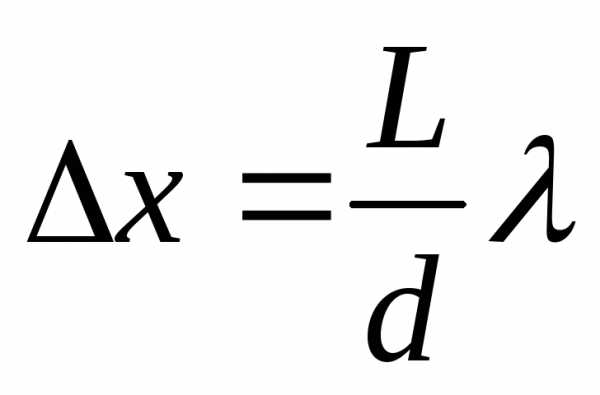 , гдеL– расстояние от когерентных источников до экрана,d- расстояние между когерентными источниками (рис. 4.6).
, гдеL– расстояние от когерентных источников до экрана,d- расстояние между когерентными источниками (рис. 4.6).
Интерференция в тонких пленках
П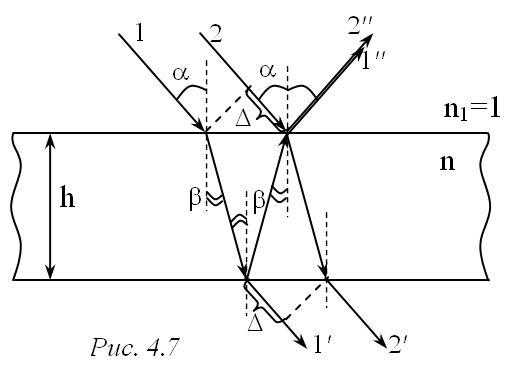 ри падении светового пучка на тонкую прозрачную пленку происходит отражение от обеих поверхностей пленки, в результате чего возникают две когерентных волны, способных интерферировать (рис. 4.7).
ри падении светового пучка на тонкую прозрачную пленку происходит отражение от обеих поверхностей пленки, в результате чего возникают две когерентных волны, способных интерферировать (рис. 4.7).
В тонких пластинках (параллельных или клиновидных) при наблюдении интерференции в проходящем свете (лучи 1΄, 2΄) разность хода будет иметь вид: или.
В отраженном свете происходит изменение фазы на π (т.к происходит отражение от границы с оптически более плотной средой) и разность хода (для лучей 1′′ и 2′′) будет иметь вид:
или.
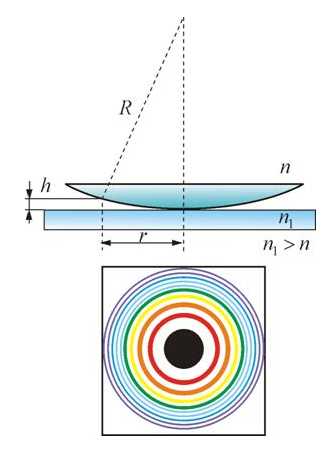
Кольца Ньютона – это система, состоящая из плосковыпуклой линзы, помещенной на стеклянную пластинку. Роль тонкой пленки играет воздушный зазор между линзой и пластинкой. При нормальном падении света на поверхность линзы будут наблюдаться чередование светлых и темных полос радиусом r. Радиус светлого кольца в проходящем свете (или темного в отраженном свете):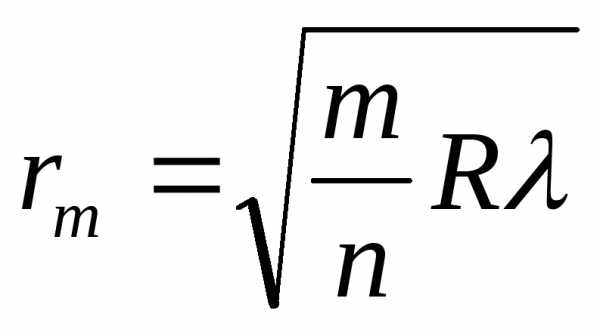
Радиус темного кольца в проходящем свете (или светлого в отраженном):
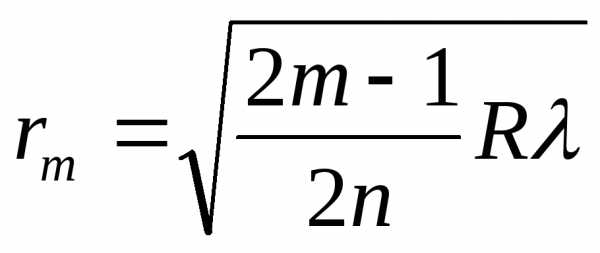 ,
,
где m– номер кольца,n– показатель преломления среды между линзой и пластинкой.
Дифракция света. Дифракция Френеля
Дифракция – это явление нарушения прямолинейного распространения света, кроме явлений, связанных с отражением и преломлением света на границе двух сред.
Френелем был разработан метод, позволяющий легко определить результирующую интенсивность световой волны в любой точке пространства. Он предложил разбить волновую поверхность на кольцевые зоны таким образом, чтобы разность хода волн от соседних зон была равна λ/2 (рис.4.8). Тогда, четное число волн, пришедших в точку наблюдения Р, дадут минимум (т.к. волны приходят в противофазе и, следовательно, гасят друг друга), а нечетное число – максимум.
Р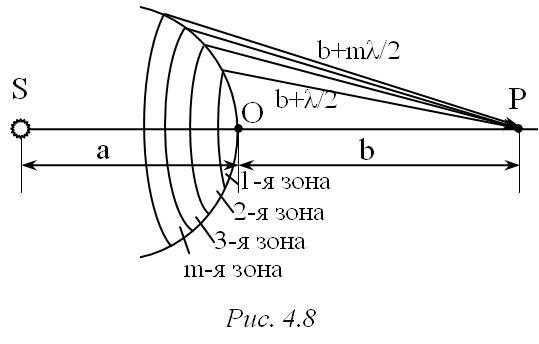 езультирующая амплитуда колебаний может быть записана как:
езультирующая амплитуда колебаний может быть записана как: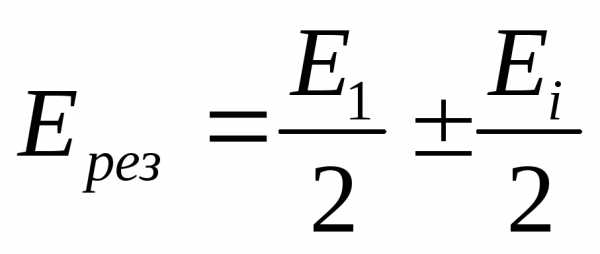 , где Е1и Еi– это амплитуды от первой и последней зоны, «+» ставится, если число зон нечетное, и «–», если четное.
, где Е1и Еi– это амплитуды от первой и последней зоны, «+» ставится, если число зон нечетное, и «–», если четное.
Радиус зоны rбудет зависеть от вида волны (плоская или сферическая) и от расстояний до зоны и после. Для сферической волны: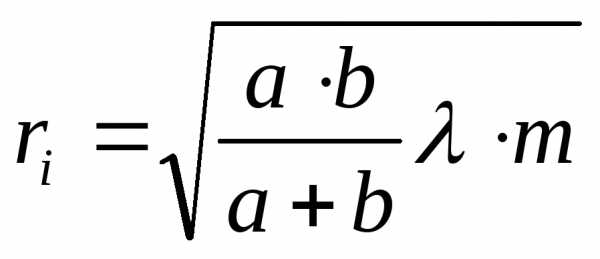 ,
,
где а- расстояние от источника до зоны, b– расстояние от зоны до точки наблюдения,m– номер зоны (рис.4.8).
Для плоской волны (а = ∞): .
В случае нормального падения на препятствие (щель) параллельного пучка лучей будет наблюдаться дифракция Фраунгофера. Условие минимума интенсивности в этом случае выглядит так: ,
где b– ширина щели, φ – угол дифракции,m– порядок дифракционного минимума, λ – длина волны.
Условие максимума: ,
где φ΄- приближенное значение угла дифракции.
Дифракционная решетка – это спектральный прибор, состоящий из большого числа одинаковых по размеру щелей, отстоящих на равных между собой промежутках. Периодом решетки (постоянная решетки) dназывают расстояние между соседними щелямиd = a+b, где а – ширина промежутка,b– ширина щели. Еще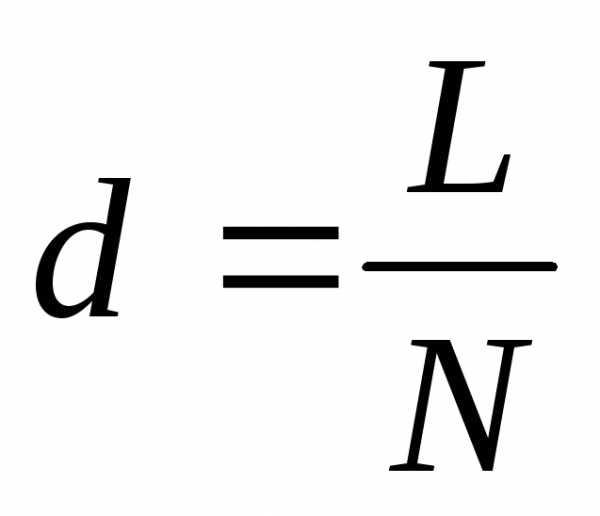 , гдеL– длина всей решетки,N – число штрихов решетки.
, гдеL– длина всей решетки,N – число штрихов решетки.
Условие главных максимумов дифракционной решетки имеет вид:
.
Разрешающая сила решетки: 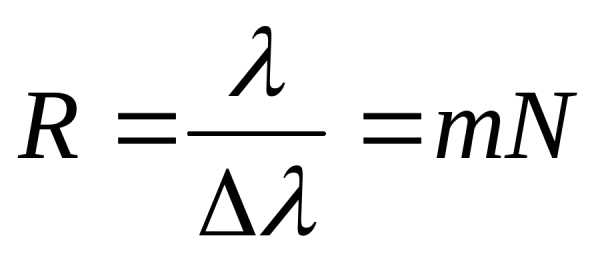 ,
,
где Δλ – наименьшая разность длин волн двух соседних спектральных линий (λ и λ+Δλ), которые можно наблюдать раздельно при помощи данной решетки; N – число штрихов решетки,m– порядок дифракционного максимума.
Угловая дисперсия решетки: 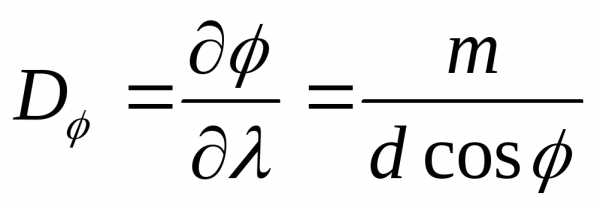 .
.
studfiles.net
35. Интерференция в тонких пленках. Просветление оптики.
Интерференция в тонкой плёнке происходит, когда падающие световые волны, отраженные от верхней и нижней границы тонкой пленки, интерферируют друг с другом, формируя новую волну. Тонкая пленка представляет собой слой материала толщиной в диапазоне от субнанометрового до микронного. Когда свет падает на поверхность пленки, он либо проходит насквозь, либо отражается от верхней поверхности. Свет, который проходит через верхнюю границу, достигает нижнюю поверхность и может вновь быть преломлен или отражён.
Просветле́ние о́птики — это нанесение на поверхность линз, граничащих с воздухом, тончайшей плёнки или нескольких слоев плёнок один поверх другого. Это позволяет увеличить светопропускание оптической системы и повысить контрастность изображения за счёт подавления бликов. Величи́ны показателей преломления чередуются по величине и подбираются таким образом, чтобы за счёт интерференции уменьшить (или совсем устранить) нежелательное отражение.
36. Полосы равного наклона.
Интерференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами, называются полосами равного наклона.
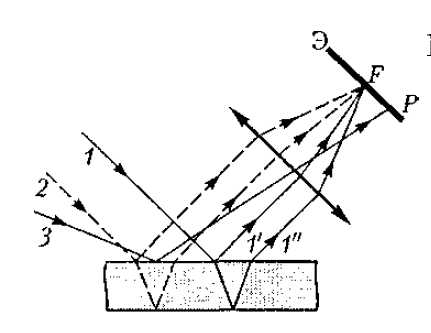
Лучи 1' и 1", отразившиеся от верхней и нижней граней пластинки, параллельны друг другу, так как пластинка плоскопараллельна. Следовательно, интерферирующие лучи 1' и 1' ' «пересекаются» только в бесконечности, поэтому говорят, что полосы равного наклона локализованы в бесконечности. Для их наблюдения используют собирающую линзу и экран (Э), расположенный в фокальной плоскости линзы.
37. Полосы равной толщины.
Для достаточно тонкой пластинки или пленки (поверхности которой не обязательно должны быть параллельными и вообще плоскими) можно наблюдать интерференционную картину, локализованную вблизи отражающей поверхности. Интерференционные полосы, возникающие в результате интерференции от мест одинаковой толщины, называются полосами равной толщины. В белом свете интерференционные полосы окрашены. Поэтому такое явление называют цветами тонких пленок. Его легко наблюдать на мыльных пузырях, на тонких пленках масла или бензина, плавающих на поверхности воды, на пленках окислов, возникающих на поверхности металлов при закалке, и т.п.
Кольца Ньютона - пример полос равной толщины. Они наблюдаются при отражении света. От соприкасающихся друг с другом плоско параллельной толстой стеклянной пластинки и плоско выпуклой линзы с большим радиусом кривизны. Роль тонкой пленки переменной толщины b, от поверхности которой отражаются когерентные волны, играет зазор между пластинкой и линзой.
38. Изменение фазы волны при отражении от границы раздела двух сред.
при отражении от более плотной фаза волны изменится на п
при отражении от менее плотной не изменится
39. Принцип Гюйгенса-Френеля.
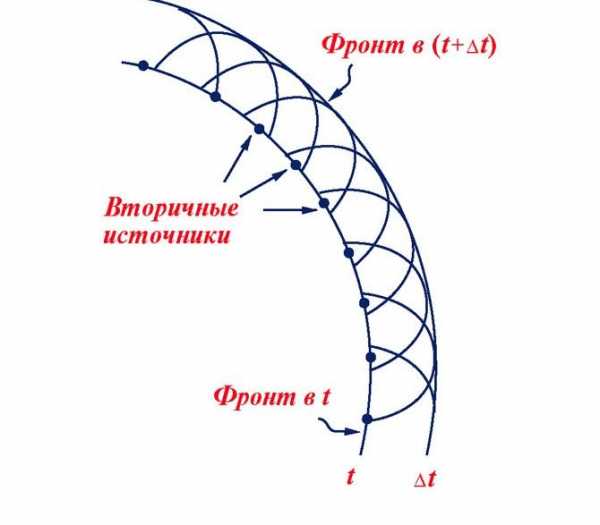
Согласно принципу Гюйгенса каждая точка пространства, до которой доходит волна, служит центром вторичных волн, огибающая которых задает положение волнового фронта в следующий момент времени.
Волновой фронт − геометрическое место точек, до которых доходят колебания к моменту времени t.
Принцип Гюйгенса решает лишь задачу о направлении распространения волнового фронта, но не затрагивает вопроса об амплитуде, (интенсивности) волн, распространяющихся по разным направлениям. Френель вложил в принцип Гюйгенса физический смысл, дополнив его идеей интерференции вторичных волн.
Интерференция света в тонких пленках
Пример интер. Света в естественных условиях –радужная окраска, например в тонких пленках(масло на поверхности воды, мыльные пузыри). Образование частич. Когерентных волн, кот. Интерферируют при наложении, происходит из за отражения света, падающего на поверхность пленки от ее верх. И нижней поверхностей. Результат интерференции зависит от сдвига фаз, которые приобретает волны, отражающ. От верх и ниж. Поверхностей пленки и в зависимости от их оптич. Разности хода.
Оптической длиной пути света Sназывается произведение геом. Длины путиl, которую проходит свет в среде на показатель преломления этот средыN(S=l*n)
Показатель преломления(абсолютный) называется величина n=c/V, гдеV- фазовая скорость в среде. Относ. Показатель преломления 2 сред- величинаn21=n2/n1. И тогда оптич. Разностью хода 2 волн называется разность оптич. Длин этих волн. /\S=S1-S2. /\Sсоответствует изменению разности фаз на величину /\Ф=2Pi*/\S/a0.
Пусть на плоскопарал. Однородную изотропную и прозрачную для света пластину толщиной dпод угломIпадает плоская монохром. Световая волна. За счет отражения света от верх. И ниж. Поверхности пластинки, в направлении отраженных лучей будут распр. 2 волны, оптич. Разностью хода которых= /\S=2dncosr-a0/2.r-угол преломления.
2dncosr=(2m+1)a0/2->2dcosr=(2m+1)a/2; m=0,1,2..;2dcosr=ma=ma0 m=1,2,3..- порядок интер. Минимума. /\s=2dncosr. И отличается от отраженного света наa0/2. максимуму отражения будут сотв. Мин. Прохождения и наоборот.
Дифракция света
1.Принцип Гюйгенса-Френеля. Прямолинейное распространение света. Дифракция света- совокупность явлений, обусловленных волновой природой света и наблюдается при распространении света в среде, с резко выраженной оптической неоднородностью.(огибание светом препятствий). Если известно положение фронта волны и известна скорость распространения волны, то положение фронта волны в новый момент времени /\t+t.
Принцип Гюйгенса: все т. поверхности S(t) через которые проходит фронт волны в момент времениt, следует рассматривать как источники вторичных волн, а положение фронтаS(/\t+t) совпадает с поверхностью огибающей вторичные волны. В однородной среде вторичные волны распространяются только вперед, т.е. в направлениях, составляющих острые углы с внешней нормалью фронта. И в однородной изотропной среде вторичные волны явл. Сферическими.
Принцип Гюйгенса-Френеля является чисто теоретическим и не указывает способы расчета амплитуды волны, которая огибает вторичные волны. Приближенный метод для расчета распр. Световых волн, которые являются развитием принципа Гюйгенса на основе, предлож. Фарадеем идеи о когерентности вторичных волн и интер. Их при наложении, называется принципом Гюйгенса-Френеля. Его можно выразить в виде следующих положений.
Лекция 4
1) При расчете амплитуды световых колебаний, которые возбуждаются источником S0 в т.М,S0 можно заменить эквивалентной системой вторичных источников. Они представляют собой малые участки поверхностиdsв любой замкнутой поверхностиS, чтобы она обхватывала источник и не охватывала рассматриваемую точку М. 2) Вторичные источники когерентны источникуS0. Поэтому вторичные волны интерферируют при наложении. Расчет интерференции прост, если вспомогательная поверхностьSявляется волновой поверхностью для света от источникаS0, т.к. при этом фазы колебаний всех вторичных источников одинаковы. 3) АмплитудаdAколебаний, которые возбуждаются в т.М вторичным источником ~ отношениюdsсоотв. Участка волновой поверхностиSи обратнопропорциональны расстояниюrот источника о т.М. И зависит от углаaмежду внешней нормалью волновой поверхности и направлению от источникаdsи т.М.dA=f(a)ads/r. Гдеa- величина ~ амплитуде первоначальной волны в т.элементах поверхностиds.f(a)- функция которая изменяется от 1, когдаa=0 доa=pi/2.
4) Если часть поверхности Sзакрыта непрозрачным экраном, то соотв. Закрыт. Экраном источники вторичных волн не излучают.
С помощью принципа Гюйгенса-Фринеля можно обосновать закон прямолинейно распределения света однородной среды. Пусть есть точечный источник света S0, который излучает монохроматический свет. В качестве вспомогательной поверхностиSвозьмем волновую поверхностьS. Разобьем поверхностьSна небольшие кольцевые участки-зоны Френеля. Колебания, которые возбуждаются в точке М 2 соседними зонами будут противоположны по фазам, т.к. разность хода от сходственных точек этих зон до т.М=a/2.
Амплитуда результирующих колебаний в т.М: A=A1-A2+A3-A4+A5…При увеличенииi, увеличивается расстояниеriот этой зоны до т.М, и при этом увеличивется уголa, между направлением нормали к поверхности этой зоны и направлением на т.М. В соответствии с этим по принципу Гюйгенса Фринеля получаем:A1<A2<A3<A4…Ai=(A[i+1]+A[i-1])/2. Тогда амплитуда световых колебаний в т.М будет равнаA1/2. результирующее действие всего волнового фронта= половине действ.Iзоны Френеля. Практически источник света излучает свет, который распространяется прямолинейно, из точкиS0 в т.М.
Если на пути монохромного света от т. источника S0 поставить экран, который закрывает все зоны Френеля для т.наблюдения кромеI, то амплитуда и интенсивность света в т.М увеличивается соответственно в 2 или 4 раза по сравнению с их значением в отсутствии экрана.I=A1*A1. Еще большее усиление света в т.М можно осуществить с помощью так называемой зоны пластинки. Это стеклянная пластинка, на поверхность нанесено непрозрачное покрытие в виде колец, кот. Закрывают только четные или нечетные зоны колец. Такая пластинка действует на свет подобно собирающей линзе.
studfiles.net
Интерференция света в тонких пленках. Просветление оптики
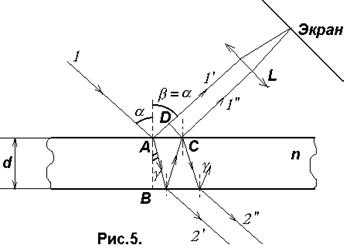 Пусть на плоскопараллельную прозрачную пленку (пластинку) с показателем преломления n и толщиной d под углом a падает плоская монохроматическая волна (для простоты рассмотрим один луч). На поверхности пленки в точке А волна частично отражается (луч 1’) и частично преломляется (луч АВ). В точке В волна также частично отражается (луч ВС) и частично преломляется (луч 2’). То же самое происходит в точке С. Причем преломленная волна (луч 1”) накладывается на волну непосредственно отраженную от верхней поверхности (луч 1’). Эти две волны когерентны, если оптическая разность хода меньше длины когерентности lког, и в этом случае они интерферируют.
Пусть на плоскопараллельную прозрачную пленку (пластинку) с показателем преломления n и толщиной d под углом a падает плоская монохроматическая волна (для простоты рассмотрим один луч). На поверхности пленки в точке А волна частично отражается (луч 1’) и частично преломляется (луч АВ). В точке В волна также частично отражается (луч ВС) и частично преломляется (луч 2’). То же самое происходит в точке С. Причем преломленная волна (луч 1”) накладывается на волну непосредственно отраженную от верхней поверхности (луч 1’). Эти две волны когерентны, если оптическая разность хода меньше длины когерентности lког, и в этом случае они интерферируют.
Оптическая разность хода двух волн D=(AB+BC)n-(AD-l/2),
где l/2 – потеря полуволны при отражении луча 1’ в точке А. Используя закон преломления n1sina = n2sing и учитывая, что в рассматриваемом случае n1=1, n2=n, можно показать, что . (17)
В точке наблюдения на экране будет максимум, если D=ml и минимум, если D = (2m+1)l/2 [см.(15), (16)].
Возможность уменьшения вредного отражения света вследствие интерференции в тонких пленках широко используется в современных оптических приборах. Для этого на передние поверхности линз, призм наносят тонкие пленки с показателем преломления n= и толщиной d, которая определяется из условия минимума при интерференции волн, отраженных от границ раздела сред с n1и n и n и n2 D=2dn=(2m+1)l/2, m=0,1,2… (18)
Минимальная толщина пленки соответствует m = 0
d=l/(4n).
Такая оптика получила название просветленной оптики.
Интерферометры и их применение
Явление интерференции света используется в ряде весьма точных измерительных приборов, получивших название интерферометров. Интерферометры используют для точного (порядка 10-7м) измерения длины тел, длины волны света, показателей преломления, для контроля чистоты обработки поверхности и др.
Лекции 4,5 Дифракция света
Это явление отклонения света от прямолинейного распространения, когда свет, огибая препятствия, заходит в область геометрической тени.
В общем случае дифракцию понимают как нарушение законов геометрической оптики, сопровождаемое интерференционными явлениями.
Природа и основные принципы дифракции могут быть установлены с помощью принципа Гюйгенса-Френеля.
Принцип Гюйгенса-Френеля
В 1678 г. Гюйгенс сформулировал правило, называемое принципом Гюйгенса: каждая точка, до которой доходит волна, является источником (центром) одной из вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени. (Напомним, что волновым фронтом называется геометрическое место точек, до которых доходят колебания к моменту времени t).
Пусть Ф(t) – фронт волны в момент времени t (см. рис. 1). Тогда, согласно принципу Гюйгенса, фронт волны в момент времени t+Dt совпадает с поверхностью огибающей всех вторичных волн. Основная слабость принципа Гюйгенса в том, что он не учитывает явления интерференции вторичных волн и, следовательно, не позволяет рассчитывать амплитуды волн, распространяющихся в различных направлениях.
Этот недостаток был устранен Френелем, который в 1815 г. дополнил принцип Гюйгенса, введя представление о когерентности вторичных волн и интерференции их между собой.
Дополненный Френелем принцип Гюйгенса называется принципом Гюйгенса-Френеля.
Метод зон Френеля
Расчет интерференции вторичных волн сводится к интегрированию, которое часто бывает затруднительным. Для упрощения вычислений при определении амплитуды волны в заданной точке пространства Френель предложил разбивать поверхность фронта волны на зоны (зоны Френеля) так, что волны от соседних зон приходят в точку наблюдения в противофазе и, вычитаясь, ослабляют друг друга.
Применим метод зон Френеля для расчета дифракции света.
Различают два случая дифракции света:
1. Дифракция Френеля или дифракция в сходящихся лучах, когда на препятствие падает плоская или сферическая волна, и дифракционная картина наблюдается на экране, находящемся на конечном расстоянии от него (см. 4.3).
2. Дифракция Фраунгофера или дифракция в параллельных лучах, когда на препятствие падает плоская волна, и дифракционная картина наблюдается на экране, который находится в фокальной плоскости собирающей линзы, установленной на пути прошедшего через препятствие света (см. 4.4).
infopedia.su
3.4. Интерференция света в тонких пленках. Просветление оптики
П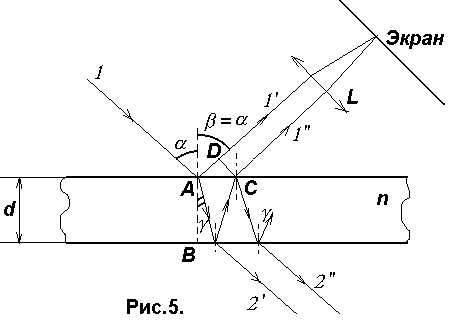 усть на плоскопараллельную прозрачную пленку (пластинку) с показателем преломленияn и толщиной d под углом падает плоская монохроматическая волна (для простоты рассмотрим один луч). На поверхности пленки в точке А волна частично отражается (луч 1’) и частично преломляется (луч АВ). В точке В волна также частично отражается (луч ВС) и частично преломляется (луч 2’). То же самое происходит в точке С. Причем преломленная волна (луч 1”) накладывается на волну непосредственно отраженную от верхней поверхности (луч 1’). Эти две волны когерентны, если оптическая разность хода
усть на плоскопараллельную прозрачную пленку (пластинку) с показателем преломленияn и толщиной d под углом падает плоская монохроматическая волна (для простоты рассмотрим один луч). На поверхности пленки в точке А волна частично отражается (луч 1’) и частично преломляется (луч АВ). В точке В волна также частично отражается (луч ВС) и частично преломляется (луч 2’). То же самое происходит в точке С. Причем преломленная волна (луч 1”) накладывается на волну непосредственно отраженную от верхней поверхности (луч 1’). Эти две волны когерентны, если оптическая разность хода  меньше длины когерентности lког, и в этом случае они интерферируют.
меньше длины когерентности lког, и в этом случае они интерферируют.
Оптическая разность хода двух волн =(AB+BC)n-(AD-/2),
где /2 – потеря полуволны при отражении луча 1’ в точке А. Используя закон преломления n1sin = n2sin и учитывая, что в рассматриваемом случае n1=1, n2=n, можно показать, что . (17)
В точке наблюдения на экране будет максимум, если m и минимум, если (2m+1)/2 [см.(15), (16)].
Возможность уменьшения вредного отражения света вследствие интерференции в тонких пленках широко используется в современных оптических приборах. Для этого на передние поверхности линз, призм наносят тонкие пленки с показателем преломления n= и толщиной d, которая определяется из условия минимума при интерференции волн, отраженных от границ раздела сред с n1 и n и n и n2 2dn=(2m+1)/2, m=0,1,2… (18)
Минимальная толщина пленки соответствуетm = 0
d=/(4n).
Такая оптика получила название просветленной оптики.
3.5. Интерферометры и их применение
Явление интерференции света используется в ряде весьма точных измерительных приборов, получивших название интерферометров. Интерферометры используют для точного (порядка 10-7м) измерения длины тел, длины волны света, показателей преломления, для контроля чистоты обработки поверхности и др.
Лекции 4,5 Дифракция света
Это явление отклонения света от прямолинейного распространения, когда свет, огибая препятствия, заходит в область геометрической тени.
В общем случае дифракцию понимают как нарушение законов геометрической оптики, сопровождаемое интерференционными явлениями.
Природа и основные принципы дифракции могут быть установлены с помощью принципа Гюйгенса-Френеля.
4.1. Принцип Гюйгенса-Френеля
В 1678 г. Гюйгенс сформулировал правило, называемое принципом Гюйгенса: каждая точка, до которой доходит волна, является источником (центром) одной из вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени. (Напомним, что волновым фронтом называется геометрическое место точек, до которых доходят колебания к моменту времени t).
ПустьФ(t) – фронт волны в момент времени t (см. рис. 1). Тогда, согласно принципу Гюйгенса, фронт волны в момент времени t+t совпадает с поверхностью огибающей всех вторичных волн. Основная слабость принципа Гюйгенса в том, что он не учитывает явления интерференции вторичных волн и, следовательно, не позволяет рассчитывать амплитуды волн, распространяющихся в различных направлениях.
Этот недостаток был устранен Френелем, который в 1815 г. дополнил принцип Гюйгенса, введя представление о когерентности вторичных волн и интерференции их между собой.
Дополненный Френелем принцип Гюйгенса называется принципом Гюйгенса-Френеля.
studfiles.net
15) Интерференция в тонких пленках
Интерференцию света по методу деления амплитуды во многих отношениях наблюдать проще, чем в опытах с делением волнового фронта. Один из способов, использующих такой метод, – опыт Поля.
В опыте Поля свет от источника S отражается двумя поверхностями тонкой прозрачной плоскопараллельной пластинки (рис. 8.7).
В любую точку P, находящуюся с той же стороны от пластинки, что и источник, приходят два луча. Эти лучи образуют интерференционную картину.
Для определения вида полос можно представить себе, что лучи выходят из мнимых изображений S1 и S2 источника S, создаваемых поверхностями пластинки. На удаленном экране, расположенном параллельно пластинке, интерференционные полосы имеют вид концентрических колец с центрами на перпендикуляре к пластинке, проходящем через источник S. Этот опыт предъявляет менее жесткие требования к размерам источника S, чем рассмотренные выше опыты. Поэтому можно в качестве S применить ртутную лампу без вспомогательного экрана с малым отверстием, что обеспечивает значительный световой поток. С помощью листочка слюды (толщиной 0,03 – 0,05 мм) можно получить яркую интерференционную картину прямо на потолке и на стенах аудитории. Чем тоньше пластинка, тем крупнее масштаб интерференционной картины, т.е. больше расстояние между полосами.
16) Дифракция света
Дифра́кция во́лн (лат. diffractus — буквально разломанный, переломанный, огибание препятствия волнами) — явление, которое проявляет себя как отклонение от законов геометрической оптики при распространении волн. Она представляет собой универсальное волновое явление и характеризуется одними и теми же законами при наблюдении волновых полей разной природы.
Дифракция неразрывно связана с явлением интерференции. Более того, само явление дифракции зачастую трактуют как случай интерференции ограниченных в пространстве волн (интерференция вторичных волн). Общим свойством всех эффектов дифракции является зависимость степени её проявления от соотношения между длиной волны λ и размером ширины волнового фронта d, либо непрозрачного экрана на пути его распространения, либо неоднородностей структуры самой волны.
Поскольку в большинстве случаев, имеющих практическое значение, это ограничение ширины волнового фронта имеет место всегда, постольку явление дифракции всегда сопровождает любой процесс распространения волн.
Так, именно явлением дифракции задаётся предел разрешающей способности любого оптического прибора, создающего изображение, который невозможно преступить принципиально при заданной ширине спектра используемого для построения изображения излучения
17) Френель
Дифра́кция Френе́ля — дифракционная картина, которая наблюдается на небольшом расстоянии от препятствия, по условиям, когда основной вклад в интерференционную картину дают границы экрана.
На рисунке схематично изображён (слева) непрозрачный экран с круглым отверстием (апертура), слева от которого расположен источник света. Изображение фиксируется на другом экране - справа. Вследствие дифракции свет, проходящий через отверстие, расходится, поэтому область, которая была затемнена по законам геометрической оптики, будет частично освещённой. В области, которая при прямолинейном распространении света была бы освещённой, наблюдаются колебания интенсивности освещения в виде концентрических колец.
Дифракционная картина для дифракции Френеля зависит от расстояния между экранами и от расположения источников света. Её можно рассчитать, считая, что каждая точка на границе апертуры излучает сферическую волну по принципу Гюйгенса. В точке наблюдения (занимаемое вторым экраном) волны или усиливают друг друга, или гасятся в зависимости от разности хода.
18) Фраунгофер
Дифракция Фраунгофера — случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды. Расстояние должно быть таким, чтобы можно было пренебречь в выражении для разности фаз членами порядка , что сильно упрощает теоретическое рассмотрение явления. Здесь— расстояние от отверстия или преграды до плоскости наблюдения,— длина волны излучения, а— радиальная координата рассматриваемой точки в плоскости наблюдения в полярной системе координат. Иными словами, дифракция Фраунгофера наблюдается тогда, когда числозон Френеля , при этом приходящие в точку волны являются практически плоскими. При наблюдении данного вида дифракции изображение объекта не искажается и меняет только размер и положение в пространстве. В противоположность этому, придифракции Френеля изображение меняет также свою форму и существенно искажается.
Дифракционные явления Фраунгофера имеют большое практическое значение, лежат в основе принципа действия многих спектральных приборов, в частности, дифракционных решёток. В последнем случае для наблюдения светового поля «в бесконечности» используются линзы или вогнутые дифракционные решетки (соответственно, экран ставится в фокальной плоскости).
19) Поляриза́ция волн — характеристика поперечных волн, описывающая поведение вектора колеблющейся величины в плоскости, перпендикулярной направлению распространения волны.
В продольной волне поляризация возникнуть не может, так как направление колебаний в этом типе волн всегда совпадают с направлением распространения.[1]
Поперечная волна характеризуется двумя направлениями: волновым вектором и вектором амплитуды, всегда перпендикулярным к волновому вектору. Волновой вектор показывает направление распространения волны, а вектор поляризации представляет собой вектор напряженности электрического поля. Так что в трёхмерном пространстве имеется ещё одна степень свободы — вращение вокруг волнового вектора.
Причиной возникновения поляризации волн может быть:
несимметричная генерация волн в источнике возмущения;
анизотропность среды распространения волн;
преломление и отражение на границе двух сред.

Зависимость мгновенных потенциалов при круговой поляризации
В общем случае для гармонических волн конец вектора колеблющейся величины описывает в плоскости, поперечной направлению распространения волны, эллипс, и такая поляризация называется эллиптической. Важными частными случаями являются линейная поляризация, при которой колебания возмущения происходят в какой-то одной плоскости, в таком случае говорят о «плоско-поляризованной волне», и круговая или циркулярная поляризация, при которой конец вектора амплитуды описывает окружность в плоскости колебаний, круговая поляризация в зависимости от направления вращения вектора может быть правой или левой.
Поляризация описывается Фигурами Лиссажу и соответствует сложению поперечных колебаний равной частоты. Закон Малюса — физический закон, выражающий зависимость интенсивности линейно-поляризованного света после его прохождения через поляризатор от угла между плоскостямиполяризации падающего света и поляризатора.
где — интенсивность падающего на поляризатор света,— интенсивность света, выходящего из поляризатора,—коэффициент пропускания поляризатора.
Установлен Э. Л. Малюсом в 1810 году.
В релятивистской форме
где и— циклические частоты линейно поляризованных волн, падающей на поляризатор и вышедшей из него.
Свет с иной (не линейной) поляризацией может быть представлен в виде суммы двух линейно-поляризованных составляющих, к каждой из которых применим закон Малюса. По закону Малюса рассчитываются интенсивности проходящего света во всех поляризационных приборах, например в поляризационных фотометрах и спектрофотометрах. Потери на отражение, зависящие от и не учитываемые законом Малюса, определяются дополнительно.
20) Фотоэффект
Фотоэффе́кт, Фотоэлектрический эффект — испускание электронов веществом под действием света (или любого другого электромагнитного излучения). В конденсированных (твёрдых и жидких) веществах выделяют внешний и внутренний фотоэффект.
Законы Столетова для фотоэффекта:
Формулировка 1-го закона фотоэффекта: Сила фототока прямо пропорциональна плотности светового потока.
Согласно 2-му закону фотоэффекта, максимальная кинетическая энергия вырываемых светом электронов линейно возрастает с частотой света и не зависит от его интенсивности.
3-й закон фотоэффекта: для каждого вещества существует красная граница фотоэффекта, то есть минимальная частота света (или максимальная длина волныλ0), при которой ещё возможен фотоэффект, и если , то фотоэффект уже не происходит.
Теоретическое объяснение этих законов было дано в 1905 году Эйнштейном. Согласно ему, электромагнитное излучение представляет собой поток отдельных квантов (фотонов) с энергией hν каждый, где h — постоянная Планка. При фотоэффекте часть падающего электромагнитного излучения от поверхности металла отражается, а часть проникает внутрь поверхностного слоя металла и там поглощается. Поглотив фотон, электрон получает от него энергию и, совершая работу выхода φ, покидает металл: где— максимальная кинетическая энергия, которую имеет электрон при вылете из металла.
Фотоэффект был объяснён в 1905 году Альбертом Эйнштейном (за что в 1921 году он, благодаря номинации шведского физика Карла Вильгельма Озеена, получил Нобелевскую премию) на основе гипотезы Макса Планка о квантовой природе света. В работе Эйнштейна содержалась важная новая гипотеза — если Планк в 1900 году предположил, что свет излучается только квантованными порциями, то Эйнштейн уже считал, что свет и существует только в виде квантованных порций. Из закона сохранения энергии, при представлении света в виде частиц (фотонов), следует формула Эйнштейна для фотоэффекта:
где φ — т. н. работа выхода (минимальная энергия, необходимая для удаления электрона из вещества), — максимальнаякинетическая энергия вылетающего электрона, — частота падающего фотона с энергией,h — постоянная Планка. Из этой формулы следует существование красной границы фотоэффекта, то есть существование наименьшей частоты (), ниже которой энергии фотона уже недостаточно для того, чтобы «выбить» электрон из металла. Суть формулы заключается в том, что энергия фотона расходуется на ионизацию атома вещества и на работу, необходимую для «вырывания» электрона, а остаток переходит в кинетическую энергию электрона.
Микроскоп укомплектовывался тремя компенсационными окулярами К-5, К-7 и К-10 (увеличения соответственно 5 Х, 7 Х и 10 Х) и четырьмя объективами с увеличениями 10 Х, 20 Х, 60 Х и 90 Х. Микроскоп имел увеличения:
с окулярами К-5 — 50 Х, 100 Х, 300 Х и 450 Х;
с окулярами К-7 — 70 Х, 140 Х, 420 Х и 630 Х;
с окулярами К-10 — 100 Х, 200 Х, 600 Х и 900 Х.
studfiles.net
Дифракция света
Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле – любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через небольшое отверстие в экранах и т.д.
Между интерференцией и дифракцией нет существенного физического различия. Оба явления заключаются в перераспределении светового потока в результате наложения (суперпозиции) волн. По историческим причинам отклонение от закона независимости световых пучков, возникающее в результате суперпозиции когерентных волн, принято называть интерференцией волн. Отклонение от закона прямолинейного распространения света, в свою очередь, принято называть дифракцией волн.
Наблюдение дифракции осуществляется обычно по следующей схеме. На пути световой волны, распространяющейся от некоторого источника, помещается непрозрачная преграда, закрывающая часть волновой поверхности световой волны. За преградой располагается экран, на котором возникает дифракционная картина.
Различают два вида дифракции. Если источник света S и точка наблюдения P расположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точку P, образуют практически параллельные пучки, говорят о дифракции в параллельных лучах или о дифракции Фраунгофера. В противном случае говорят о дифракции Френеля. Дифракцию Фраунгофера можно наблюдать, поместив за источником света S и перед точкой наблюдения P по линзе так, чтобы точки S и P оказались в фокальной плоскости соответствующей линзы (рис.).
Принципиально дифракция Фраунгофера не отличается от дифракции Френеля. Количественный критерий, позволяющий установить, какой вид дифракции имеет место, определяется величиной безразмерного параметра 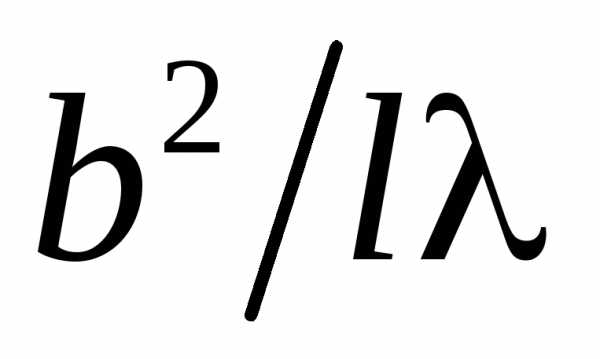 , гдеb – характерный размер препятствия, l – расстояние между препятствием и экраном, на котором наблюдается дифракционная картина, – длина волны. Если
, гдеb – характерный размер препятствия, l – расстояние между препятствием и экраном, на котором наблюдается дифракционная картина, – длина волны. Если
Явление дифракции качественно объясняется с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени. Для монохроматической волны волновая поверхность есть поверхность, на которой колебания совершаются в одинаковой фазе.
Пусть плоская волна нормально падает на отверстие в непрозрачном экране (рис.). Согласно Гюйгенсу, каждая точка выделяемого отверстием участка волнового фронта служит источником вторичных волн (в изотропной среде они сферические). Построив огибающую вторичных волн для некоторого момента времени, видим, что фронт волны заходит в область геометрической тени, т.е. огибает края отверстия.
Принцип Гюйгенса решает лишь задачу о направлении распространения волнового фронта, но не затрагивает вопроса об амплитуде, а, следовательно, и об интенсивности на фронте волны. Из повседневного опыта известно, что в большом числе случаев лучи света не отклоняются от их прямолинейного распространения. Так, предметы, освещенные точечным источником света, дают резкую тень. Таким образом, принцип Гюйгенса нуждается в дополнении, позволяющем определять интенсивность волны.
Френель дополнил принцип Гюйгенса идеей интерференции вторичных волн. Согласно принципу Гюйгенса-Френеля, световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, излучаемых малыми элементами некоторой замкнутой поверхности, охватывающей источник S. Обычно в качестве этой поверхности выбирают одну из волновых поверхностей, поэтому источники вторичных волн действуют синфазно. В аналитическом виде для точечного источника этот принцип записывается в виде
, (1) гдеE – световой вектор, включающий в себя временную зависимость 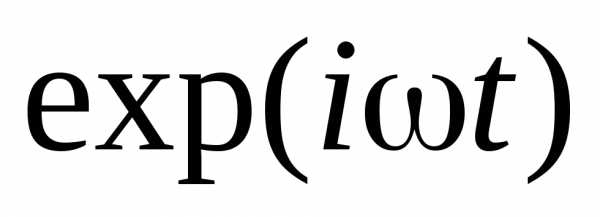 ,k – волновое число, r – расстояние от точки P на поверхности S до точки P, K – коэффициент, зависящий от ориентации площадки по отношению к источнику и точке P. Правомерность формулы (1) и вид функции K устанавливается в рамках электромагнитной теории света (в оптическом приближении).
,k – волновое число, r – расстояние от точки P на поверхности S до точки P, K – коэффициент, зависящий от ориентации площадки по отношению к источнику и точке P. Правомерность формулы (1) и вид функции K устанавливается в рамках электромагнитной теории света (в оптическом приближении).
В том случае, когда между источником S и точкой наблюдения P имеются непрозрачные экраны с отверстиями, действие этих экранов может быть учтено следующим образом. На поверхности непрозрачных экранов амплитуды вторичных источников считаются равными нулю; в области отверстий амплитуды источников такие же, как при отсутствии экрана (так называемое приближение Кирхгофа).
Метод зон Френеля. Учет амплитуд и фаз вторичных волн позволяет в принципе найти амплитуду результирующей волны в любой точке пространства и решить задачу о распространении света. В общем случае расчет интерференции вторичных волн по формуле (1) довольно сложный и громоздкий. Однако ряд задач можно решить, применив чрезвычайно наглядный прием, заменяющий сложные вычисления. Метод этот получил название метода зон Френеля.
Суть метода разберем на примере точечного источника света S. Волновые поверхности представляют собой в этом случае концентрические сферы с центром в S. Разобьем изображенную на рисунке волновую поверхность на кольцевые зоны, построенные так, что расстояния от краев каждой зоны до точки P отличаются на 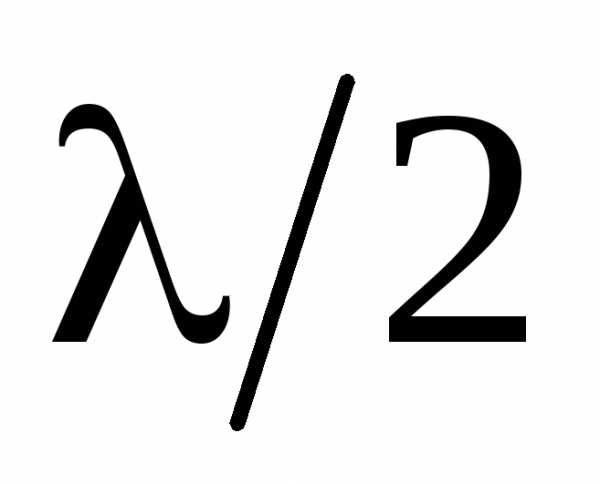 . Обладающие таким свойством зоны называютсязонами Френеля. Из рис. видно, что расстояние
. Обладающие таким свойством зоны называютсязонами Френеля. Из рис. видно, что расстояние 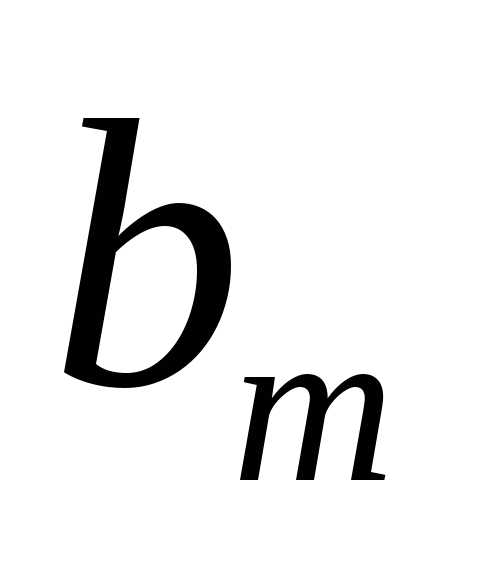 от внешнего края –m-й зоны до точки P равно
от внешнего края –m-й зоны до точки P равно
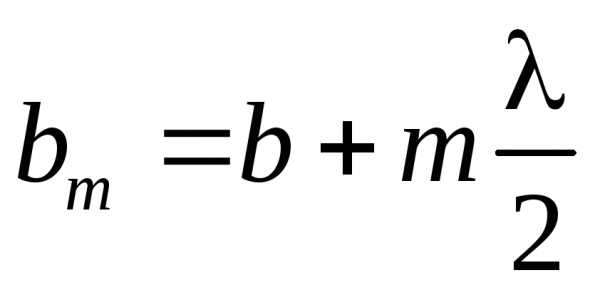 , гдеb – расстояние от вершины волновой поверхности O до точки P.
, гдеb – расстояние от вершины волновой поверхности O до точки P.
Колебания, приходящие в точку P от аналогичных точек двух соседних зон (например, точек, лежащих в середине зон или у внешних краев зон), находятся в противофазе. Поэтому колебания от соседних зон будут взаимно ослаблять друг друга и амплитуда результирующего светового колебания в точке P
, (2) где ,
, , … – амплитуды колебаний, возбуждаемых 1-й, 2-й, … зонами.
, … – амплитуды колебаний, возбуждаемых 1-й, 2-й, … зонами.
Для оценки амплитуд колебаний найдем площади зон Френеля. Пусть внешняя граница m-й зоны выделяет на волновой поверхности сферический сегмент высоты 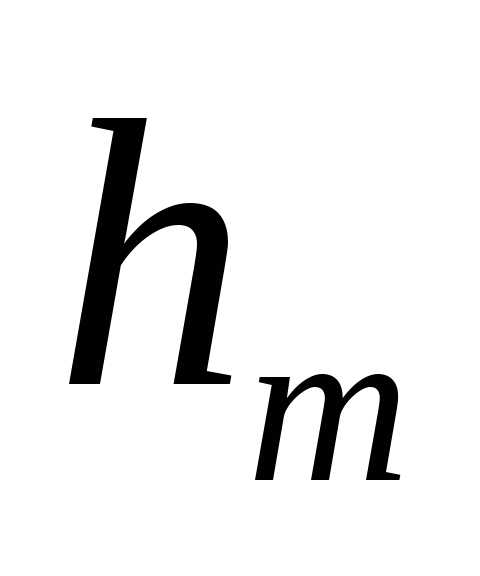 . Обозначив площадь этого сегмента через
. Обозначив площадь этого сегмента через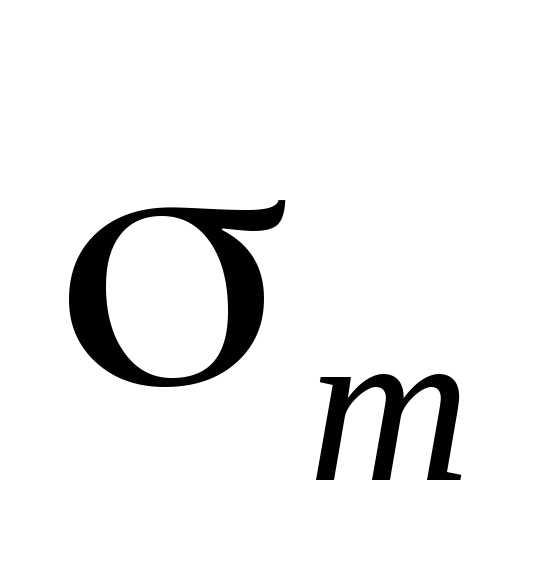 , найдем, что, площадьm-й зоны Френеля равна . Из рисунка видно, что. После несложных преобразований, учитывая
, найдем, что, площадьm-й зоны Френеля равна . Из рисунка видно, что. После несложных преобразований, учитывая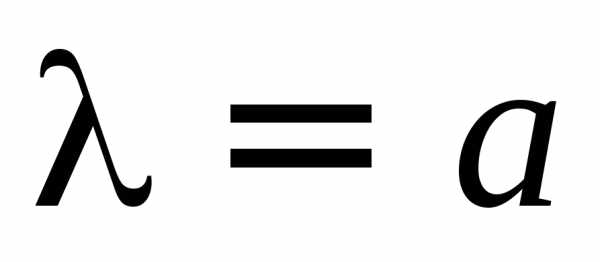 и
и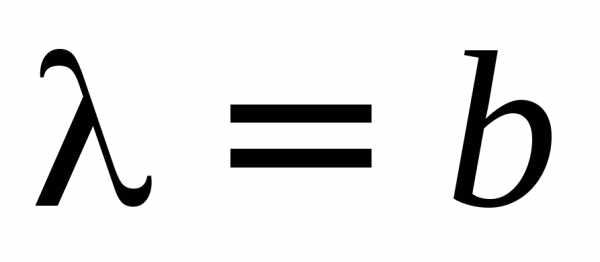 , получим
, получим
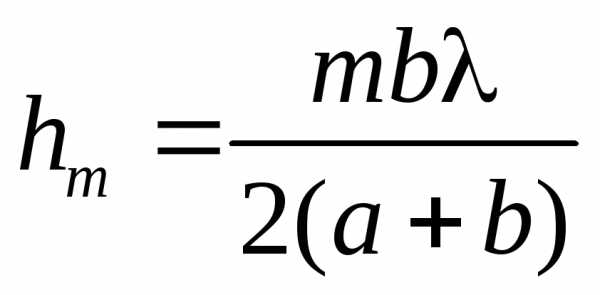 . Площадь сферического сегмента и площадьm-й зоны Френеля соответственно равны
. Площадь сферического сегмента и площадьm-й зоны Френеля соответственно равны
,. (3) Таким образом, при не слишком большихm площади зон Френеля одинаковы. Согласно предположению Френеля, действие отдельных зон в точке P тем меньше, чем больше угол  между нормальюn к поверхности зоны и направлением на P, т.е. действие зон постепенно убывает от центральной к периферийным. Кроме того, интенсивность излучения в направлении точки P уменьшается с ростом m и вследствие увеличения расстояния от зоны до точки P. Таким образом, амплитуды колебаний образуют монотонно убывающую последовательность
между нормальюn к поверхности зоны и направлением на P, т.е. действие зон постепенно убывает от центральной к периферийным. Кроме того, интенсивность излучения в направлении точки P уменьшается с ростом m и вследствие увеличения расстояния от зоны до точки P. Таким образом, амплитуды колебаний образуют монотонно убывающую последовательность
.
Общее число зон Френеля, умещающихся на полусфере, очень велико; например, при ичисло зон достигает ~106. Это означает, что амплитуда убывает очень медленно и поэтому можно приближенно считать
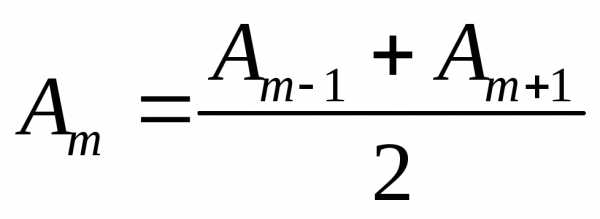 . (4) Тогда выражение (2) после перегруппировки суммируется
. (4) Тогда выражение (2) после перегруппировки суммируется
, (5) так как выражения в скобках, согласно (4), равны нулю, а вклад последнего слагаемого ничтожно мал. Таким образом, амплитуда результирующих колебаний в произвольной точкеP определяется как бы половинным действием центральной зоны Френеля.
При не слишком больших m высота сегмента 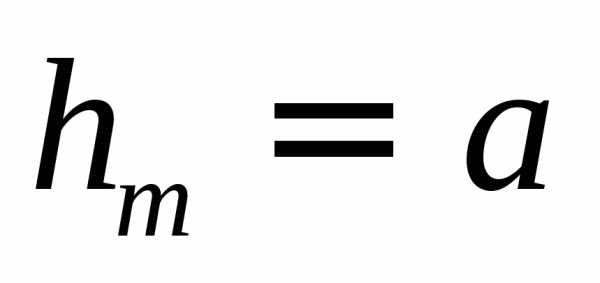 , поэтому можно считать, что
, поэтому можно считать, что . Подставив значение для
. Подставив значение для , получим для радиуса внешней границыm-й зоны
, получим для радиуса внешней границыm-й зоны
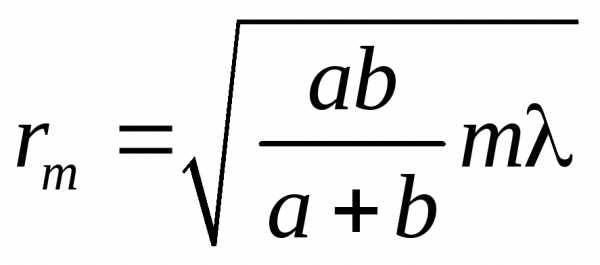 . (6) Приирадиус первой (центральной) зоны. Следовательно, распространение света отS к P происходит так, как если бы световой поток шел внутри очень узкого канала вдоль SP, т.е. прямолинейно.
. (6) Приирадиус первой (центральной) зоны. Следовательно, распространение света отS к P происходит так, как если бы световой поток шел внутри очень узкого канала вдоль SP, т.е. прямолинейно.
Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально. Для этого используются зонная пластинка – в простейшем случае стеклянная пластинка, состоящая из системы чередующихся прозрачных и непрозрачных концентрических колец, с радиусами зон Френеля заданной конфигурации. Если поместить зонную пластинку в строго определенном месте (на расстоянии a от точечного источника и на расстоянии b от точки наблюдения), то результирующая амплитуда будет больше, чем при полностью открытом волновом фронте.
Дифракция Френеля на круглом отверстии. Дифракция Френеля наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию, в данном случае экрана с отверстием. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути экран с отверстием. Дифракционная картина наблюдается на экране, параллельном экрану с отверстием. Ее вид зависит от расстояния между отверстием и экраном (для данного диаметра отверстия). Проще определить амплитуду световых колебаний в центре картины. Для этого разобьем открытую часть волновой поверхности на зоны Френеля. Амплитуда колебания, возбуждаемая всеми зонами равна
, (7) где знак плюс отвечает нечетнымm и минус – четным m.
Когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в центральной точке будет больше, чем при свободном распространении волны; если четное то амплитуда (интенсивность) будет равна нулю. Например, если отверстие открывает одну зону Френеля, амплитуда 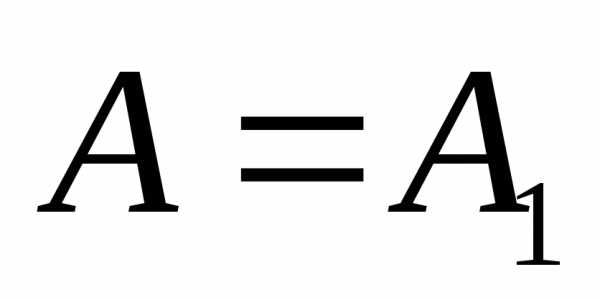 , то интенсивность (
, то интенсивность (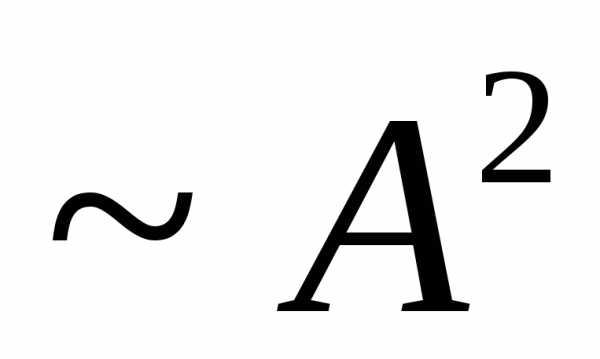 ) больше в четыре раза.
) больше в четыре раза.
Расчет амплитуды колебания на внеосевых участках экрана более сложен, так как соответствующие зоны Френеля частично перекрываются непрозрачным экраном. Качественно ясно, что дифракционная картина будет иметь вид чередующихся темных и светлых колец с общим центром (если m четное, то в центре будет темное кольцо, если m нечетное – то светлое пятно), причем интенсивность в максимумах убывает с расстоянием от центра картины. Если отверстие освещается не монохроматическим светом, а белым светом, то кольца окрашены.
Рассмотрим предельные случаи. Если отверстие открывает лишь часть центральной зоны Френеля, на экране получается размытое светлое пятно; чередования светлых и темных колец в этом случае не возникает. Если отверстие открывает большое число зон, то 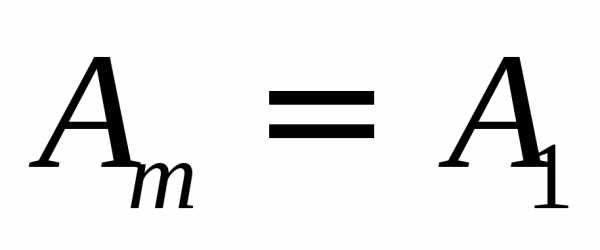 и амплитуда в центре
и амплитуда в центре , т.е. такая же, как и при полностью открытом волновом фронте; чередование светлых и темных колец происходит лишь в очень узкой области на границе геометрической тени. Фактически дифракционная картина не наблюдается, и распространение света, по сути, является прямолинейным.
, т.е. такая же, как и при полностью открытом волновом фронте; чередование светлых и темных колец происходит лишь в очень узкой области на границе геометрической тени. Фактически дифракционная картина не наблюдается, и распространение света, по сути, является прямолинейным.
Дифракция Френеля на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск (рис.). Дифракционная картина, наблюдаемая на экране, является центрально симметричной. Определим амплитуду световых колебаний в центре. Пусть диск закрывает m первых зон Френеля. Тогда амплитуда колебаний равна
или, (8) так как выражения, стоящие в скобках, равны нулю. Следовательно, в центре всегда наблюдается дифракционный максимум (светлое пятно), соответствующий половине действия первой открытой зоны Френеля. Центральный максимум окружен концентрическими с ним темными и светлыми кольцами. При небольшом числе закрытых зон амплитуда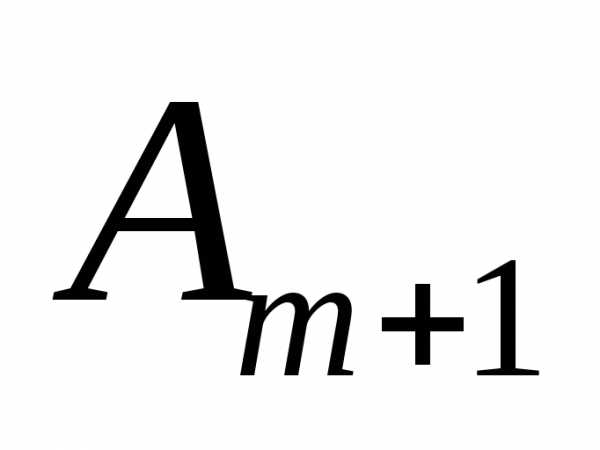 мало отличается от
мало отличается от . Поэтому интенсивность в центре будет почти такая же, как при отсутствии диска. Изменение освещенности экрана с расстоянием от центра картины изображено на рис.
. Поэтому интенсивность в центре будет почти такая же, как при отсутствии диска. Изменение освещенности экрана с расстоянием от центра картины изображено на рис.
Рассмотрим предельные случаи. Если диск закрывает лишь небольшую часть центральной зоны Френеля, он совсем не отбрасывает тени – освещенность экрана всюду остается такой же, как при отсутствии диска. Если диск закрывает много зон Френеля, чередование светлых и темных колец наблюдается только в узкой области на границе геометрической тени. В этом случае 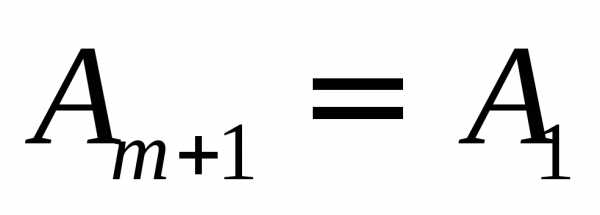 , так что светлое пятно в центре отсутствует, и освещенность в области геометрической тени практически всюду равна нулю. Фактически дифракционная картина не наблюдается, и распространение света является прямолинейным.
, так что светлое пятно в центре отсутствует, и освещенность в области геометрической тени практически всюду равна нулю. Фактически дифракционная картина не наблюдается, и распространение света является прямолинейным.
Дифракция Фраунгофера на одной щели. Пусть плоская монохроматическая волна падает нормально плоскости узкой щели шириной a. Оптическая разность хода между крайними лучами, идущими от щели в некотором направлении
.
Разобьем открытую часть волновой поверхности в плоскости щели на зоны Френеля, имеющие вид равновеликих полос, параллельных щели. Так как ширина каждой зоны выбирается такой, чтобы разность хода от краев этих зон была равна 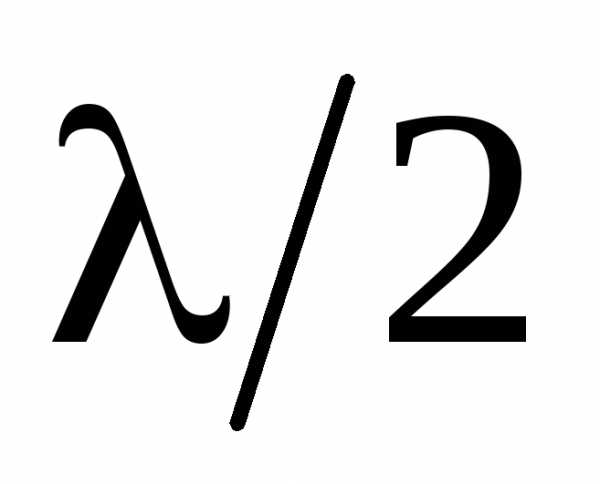 , то на ширине щели уместится
, то на ширине щели уместится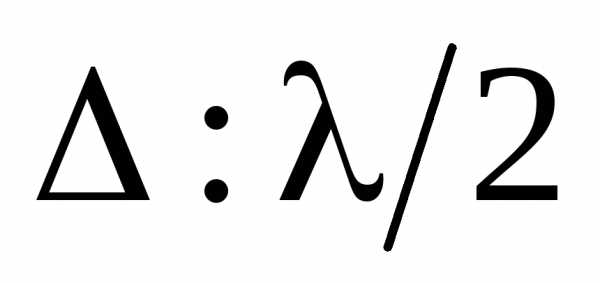 зон. Амплитуды вторичных волн в плоскости щели будут равны, так как зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения. Фазы колебаний от пары соседних зон Френеля отличаются на, поэтому, суммарная амплитуда этих колебаний равна нулю.
зон. Амплитуды вторичных волн в плоскости щели будут равны, так как зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения. Фазы колебаний от пары соседних зон Френеля отличаются на, поэтому, суммарная амплитуда этих колебаний равна нулю.
Если число зон Френеля четное, то
, (9а) и в точкеB наблюдается минимум освещенности (темный участок), если же число зон Френеля нечетное, то
(9б) и наблюдается близкая к максимуму освещенность, соответствующей действию одной нескомпенсированной зоны Френеля. В направлении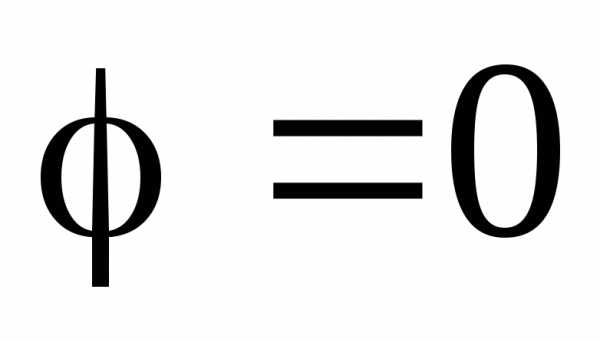 щель действует, как одна зона Френеля, и в этом направлении наблюдается наибольшая освещенность, точке
щель действует, как одна зона Френеля, и в этом направлении наблюдается наибольшая освещенность, точке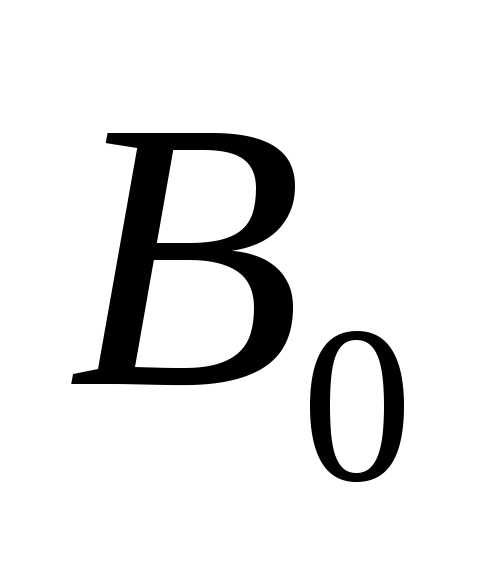 соответствует центральный или главный максимум освещенности.
соответствует центральный или главный максимум освещенности.
Расчет освещенности в зависимости от направления дает
, (10) где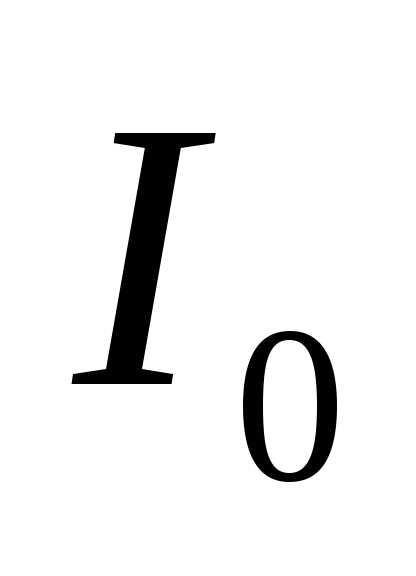 – освещенность в середине дифракционной картины (против центра линзы),
– освещенность в середине дифракционной картины (против центра линзы),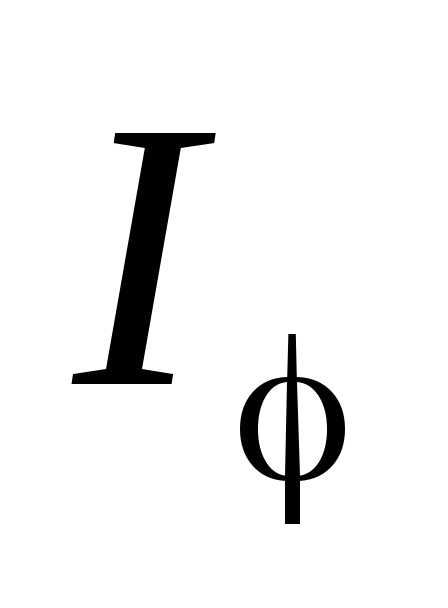 – освещенность в точке, положение которой определяется направлением. График функции (10) изображен на рис. Максимумы освещенности соответствуют значениям , удовлетворяющие условиям
– освещенность в точке, положение которой определяется направлением. График функции (10) изображен на рис. Максимумы освещенности соответствуют значениям , удовлетворяющие условиям
,,и т.д. Вместо этих условий для максимумов приближенно можно пользоваться соотношением (9б), дающим близкие значения углов. Величина вторичных максимумов быстро убывает. Численные значения интенсивностей главного и следующих максимумов относятся как
и т.д., т.е. основная часть световой энергии, прошедшей через щель, сосредоточена в главном максимуме.
Сужение щели приводит к тому, что центральный максимум расплывается, а его освещенность уменьшается. Наоборот, чем щель шире, тем картина ярче, но дифракционные полосы уже, а число самих полос больше. При  в центре получается резкое изображение источника света, т.е. имеет место прямолинейное распространение света.
в центре получается резкое изображение источника света, т.е. имеет место прямолинейное распространение света.
Дифракция Фраунгофера на дифракционной решетке. Дифракционная решетка представляет собой систему одинаковых щелей, разделенных равными по ширине непрозрачными промежутками. Дифракционную картину от решетки можно рассматривать как результат взаимной интерференции волн, идущих от всех щелей, т.е. в дифракционной решетке осуществляется многолучевая интерференция.
Рассмотрим дифракционную решетку. Если ширина каждой щели равна a, а ширина непрозрачных участков между щелями b, то величина называетсяпериодом дифракционной решетки.
Согласно формуле для многолучевой интерференции (Л3-3-5) освещенность в условиях интерференции световых лучей от N щелей равна
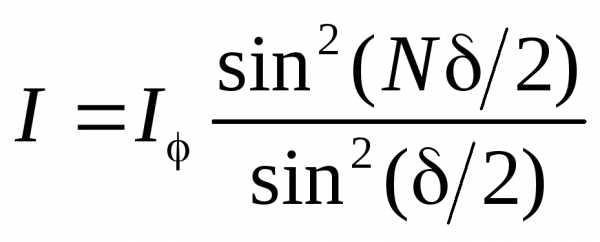 . (1) Из рис. видно, что разность хода от соседних щелей равна. Следовательно разность фаз
. (1) Из рис. видно, что разность хода от соседних щелей равна. Следовательно разность фаз
, (2) где – длина волны в данной среде. Подставив в формулу (1) выражение для  (освещенность от одной щели) и (2) для, получим
(освещенность от одной щели) и (2) для, получим
(3) (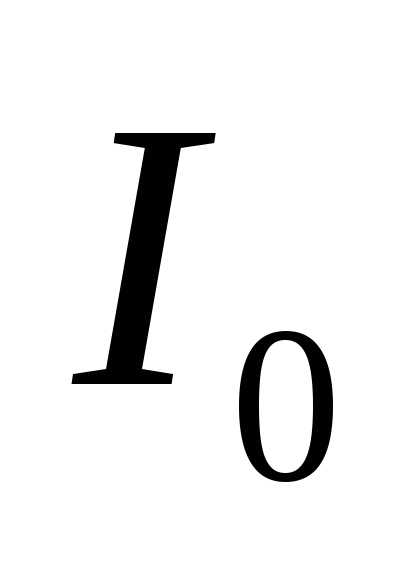 – освещенность, создаваемая одной щелью на оси линзы).
– освещенность, создаваемая одной щелью на оси линзы).
Первый множитель обращается в нуль в точках, для которых
. (4) В этих точках освещенность, создаваемая каждой из щелей в отдельности, равна нулю. Будут наблюдатьсяглавные минимумы освещенности.
Второй множитель в правой части (3) принимает экстремальное, а все выражение близкое к экстремальному, значение (локальный максимум) в точках, удовлетворяющих условию
. (5) Для направлений, определяемых этим условием, колебания от отдельных щелей взаимно усиливают друг друга. Условие (5) с достаточной точностью определяет положенияглавных максимумов. Число m дает порядок главного максимума.
Кроме главных минимумов в промежутке между соседними главными максимумами имеется  дополнительный минимум. Эти минимумы соответствуют направлениям, при которых второй множитель обращается в нуль. В данных направлениях колебания от отдельных щелей взаимно погашают друг друга. В соответствии с (3) направления дополнительных минимумов определяются условием
дополнительный минимум. Эти минимумы соответствуют направлениям, при которых второй множитель обращается в нуль. В данных направлениях колебания от отдельных щелей взаимно погашают друг друга. В соответствии с (3) направления дополнительных минимумов определяются условием
. (6) В формуле (6)m принимает все целочисленные значения кроме , т.е. кроме тех, при которых условие (6) переходит в (5).
Между дополнительными минимумами располагаются 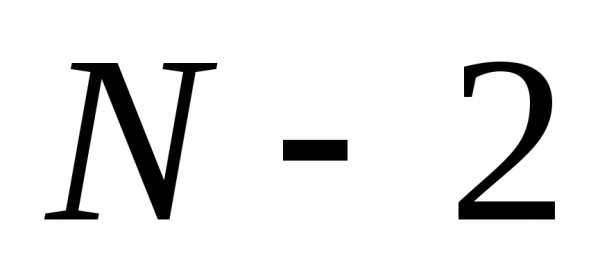 слабых вторичных максимумов. Интенсивность вторичных максимумов не превышает
слабых вторичных максимумов. Интенсивность вторичных максимумов не превышает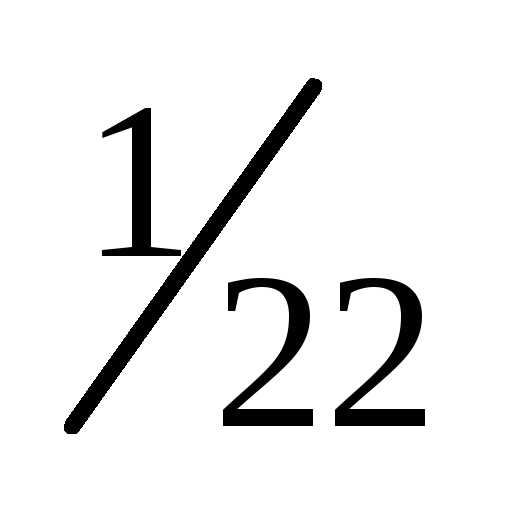 интенсивности ближайшего главного максимума (см. Л3-3). На рис. качественно представлена дифракционная картина от четырех щелей.
интенсивности ближайшего главного максимума (см. Л3-3). На рис. качественно представлена дифракционная картина от четырех щелей.
Так как , то из (4) следует, что наибольший порядок главного максимума
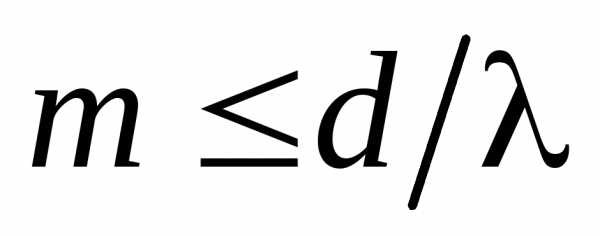 , т.е. определяется отношением периода решетки к длине волны. Положение главных максимумов зависит от длины волны. Поэтому при пропускании через решетку белого света все максимумы, кроме центрального (
, т.е. определяется отношением периода решетки к длине волны. Положение главных максимумов зависит от длины волны. Поэтому при пропускании через решетку белого света все максимумы, кроме центрального (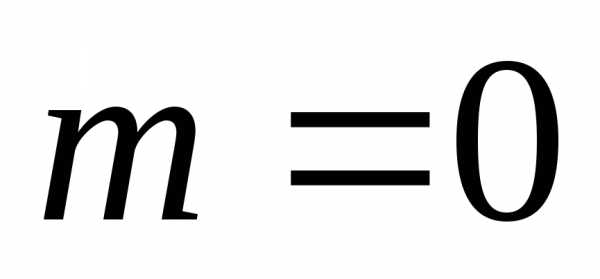 ), разложатся в спектр, фиолетовая область которого будет обращена к центру дифракционной картины, красная – наружу. Это свойство дифракционной решетки используется для исследования спектрального состава света (определения длин волн и интенсивностей всех монохроматических компонентов), т.е. дифракционная решетка может быть использована как спектральный прибор.
), разложатся в спектр, фиолетовая область которого будет обращена к центру дифракционной картины, красная – наружу. Это свойство дифракционной решетки используется для исследования спектрального состава света (определения длин волн и интенсивностей всех монохроматических компонентов), т.е. дифракционная решетка может быть использована как спектральный прибор.
Основными характеристиками всякого спектрального прибора является его дисперсия и разрешающая сила. Дисперсия определяет угловое или линейной расстояние между двумя спектральными линиями, отличающимися по длине волны на единицу (например, на 1 Å). Разрешающая сила определяет минимальную разность длин волн , при которой две линии воспринимаются в спектре раздельно.
Угловой дисперсией называется величина
, где – угловое расстояние между спектральными линиями, отличающимися по длине волны на . С помощью (4), опуская знаки, получим
. Отсюда, в пределах небольших углов (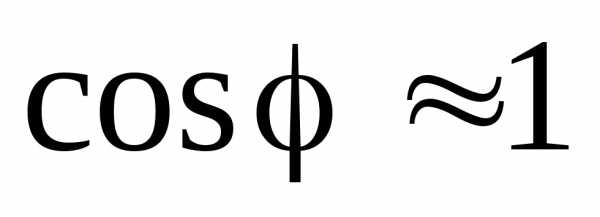 ),
),
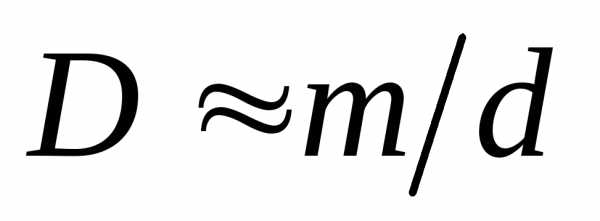 . (7)
. (7)
Разрешающей силой спектрального прибора называют безразмерную величину
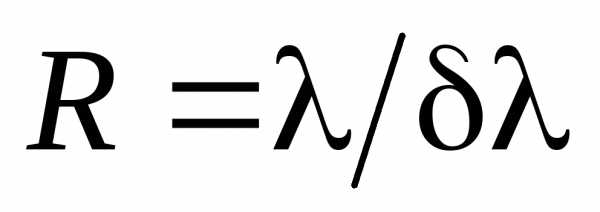 , где – минимальная разность длин волн двух спектральных линий, при которой эти линии воспринимаются раздельно.
, где – минимальная разность длин волн двух спектральных линий, при которой эти линии воспринимаются раздельно.
Согласно критерию Рэлея, изображения двух близлежащих одинаковых точечных источников или двух близлежащих спектральных линий с равными интенсивностями разрешимы (разделены для восприятия), если центральный максимум от одного источника (линии) совпадает с первым минимумом дифракционной картины от другого (рис.). При выполнении критерия Рэлея интенсивность “провала” между максимумами составляет 80 % интенсивности в максимуме, что является достаточным для разрешения источников (линий).
Положение m-го максимума для длины волны 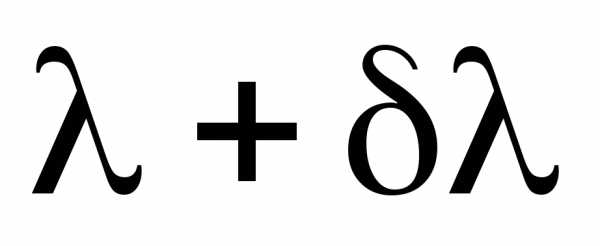 и минимума, следующего заm-м максимумом для длины волны , определяется соответственно условиями
и минимума, следующего заm-м максимумом для длины волны , определяется соответственно условиями
. Согласно критерию Рэлея две эти линии разрешаются спектральным прибором, если правые части этих соотношений равны между собой или
. Отсюда, для разрешающей силы получим выражение
. (8) Современные дифракционные решетки обладают довольно высокой разрешающей способностью (до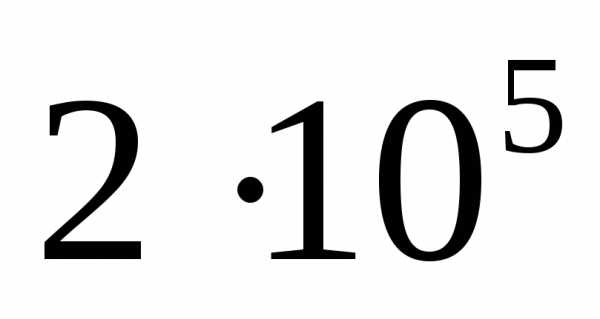 ).
).
Разрешающая сила объектива. Используя даже идеальную оптическую систему невозможно получить стигматическое изображение точечного источника, что объясняется волновой природой света. Если на объектив падает свет от удаленного точечного источника, то вследствие дифракции световых волн, в фокальной плоскости объектива вместо точки наблюдается дифракционная картина. В результате точечный источник отображается в виде светлого пятна, окруженного чередующимися темными и светлыми кольцами. Соответствующий расчет (дифракции Фраунгофера на круглом отверстии) дает, что первый минимум отстоит от центра дифракционной картины на угловое расстояние
, гдеD – диаметр объектива (или диафрагмы). Полезно сравнить этот результат с подобным результатом для дифракции на щели. В последнем случае , гдеa – ширина щели. Если  , можно положить
, можно положить
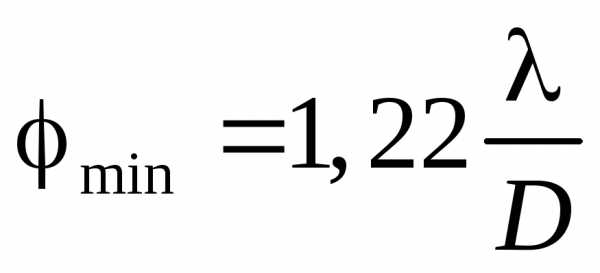 .
.
Если на объектив падает свет от двух удаленных точечных источников 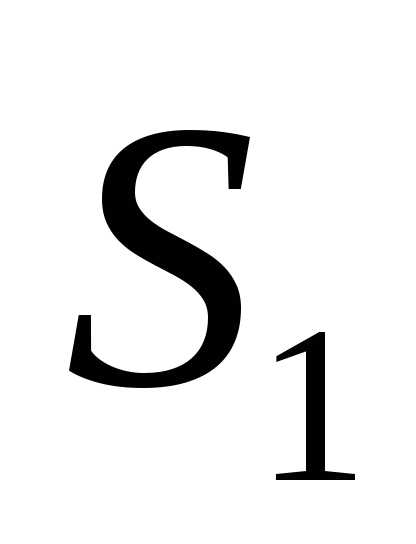 и
и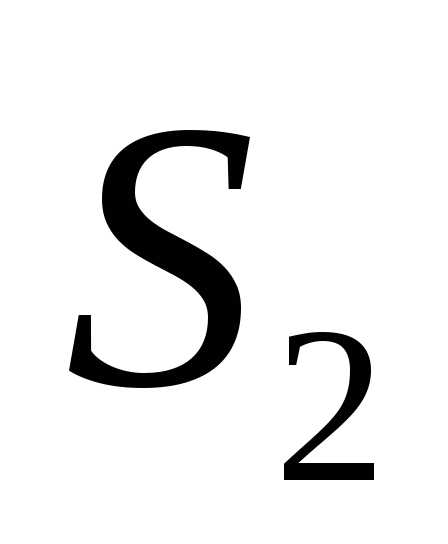 с некоторым угловым расстоянием
с некоторым угловым расстоянием , то имеет место наложение их дифракционных картин (рис.). Согласно критерию Рэлея, который в данном случае гласит что, две близкие точки будут еще разрешены, если середина центрального максимума для одной точки совпадает с первым минимумом для второй точки. Таким образом, наименьшее угловое расстояние между двумя точками, при котором они еще разрешаются объективом
, то имеет место наложение их дифракционных картин (рис.). Согласно критерию Рэлея, который в данном случае гласит что, две близкие точки будут еще разрешены, если середина центрального максимума для одной точки совпадает с первым минимумом для второй точки. Таким образом, наименьшее угловое расстояние между двумя точками, при котором они еще разрешаются объективом
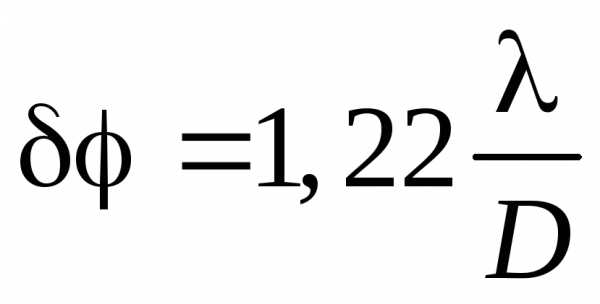 . (9) Величина, обратная, называется разрешающей силой объектива
. (9) Величина, обратная, называется разрешающей силой объектива
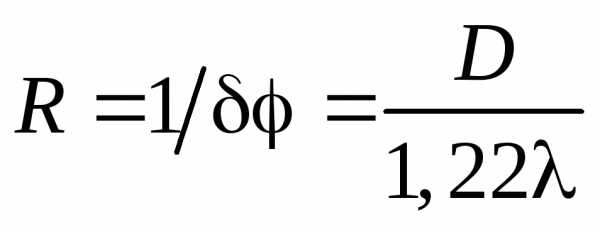 . (10)
. (10)
Диаметр зрачка глаза при нормальном освещении равен примерно 2 мм. Подставив это значение в формулу (9) и взяв , получим
. Примечательно, что расстояние между соседними светочувствительными элементами сетчатки глаза соответствует этому угловому расстоянию.
Дифракция рентгеновских лучей. Дифракция наблюдается не только на одномерной дифракционной решетке, но также трехмерных периодичных структурах. Подобными структурами являются все кристаллические тела. Однако их период (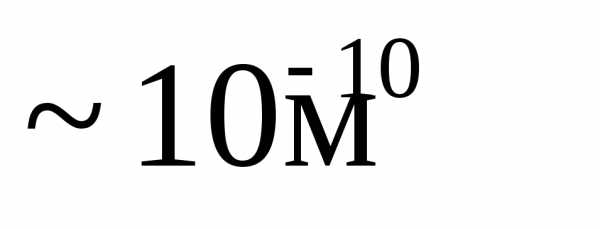 ) слишком мал для того, чтобы можно было наблюдать дифракцию в видимом свете. В случае кристаллов соотношение
) слишком мал для того, чтобы можно было наблюдать дифракцию в видимом свете. В случае кристаллов соотношение 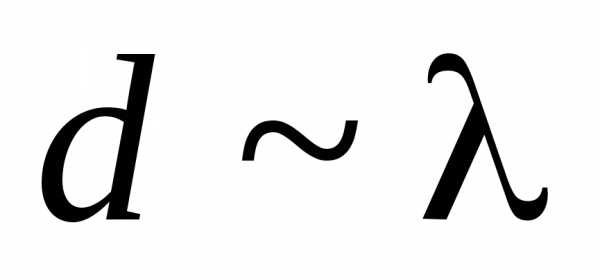 выполняется только для рентгеновских лучей.
выполняется только для рентгеновских лучей.
В случае света лучи сводятся при помощи линзы. Для рентгеновских лучей осуществить линзу невозможно, так как показатель преломления этих лучей во всех веществах практически равен единице. Поэтому интерференция вторичных волн достигается путем использования весьма узких пучков лучей, которые и без линзы дают на экране (или фотопластинке) пятна очень малых размеров.
Рассматриваем кристалл как совокупность параллельных кристаллографических плоскостей (плоскостей, в которых лежат узлы кристаллической решетки), отстоящих друг от друга на расстояние d. Полагаем, что при падении рентгеновского излучения на кристалл происходит частичное отражение излучения от этих плоскостей. Вторичные волны, отразившиеся от разных плоскостей, когерентны и будут интерферировать между собой. Из рис. видно, что разность хода двух волн, отразившихся от соседних плоскостей, равна 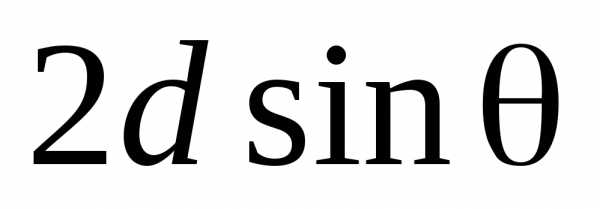 , где – угол, называемый углом скольжения падающих лучей. Максимумы интенсивности (дифракционные максимумы) наблюдаются в тех направлениях, в которых все отраженные атомными плоскостями волны будут находиться в одинаковой фазе. Эти направления определяются условием
, где – угол, называемый углом скольжения падающих лучей. Максимумы интенсивности (дифракционные максимумы) наблюдаются в тех направлениях, в которых все отраженные атомными плоскостями волны будут находиться в одинаковой фазе. Эти направления определяются условием
. (11) Это соотношение называетсяВульфа-Брегга.
Кристаллографические плоскости можно провести в кристалле множеством способов (рис.). Каждая система плоскостей может дать дифракционный максимум, если для нее окажется выполненным условие (11). Однако заметную интенсивность имеет лишь те максимумы, которые дают плоскости с густо расположенными узлами.
Дифракция рентгеновских лучей от кристаллов находит два основных применения. Она используется для исследования спектрального состава рентгеновского излучения (рентгеновская спектроскопия) и для изучения структуры кристаллов (рентгеноструктурный анализ). Определяя направления максимумов, получающихся при дифракции исследуемого рентгеновского излучения от кристаллов с известной структурой, можно вычислить длины волн. Наблюдая дифракцию рентгеновских лучей известной длины волны на кристалле неизвестного строения можно найти межплоскостные расстояния и расшифровать структуру кристалла.
Голография. Голография есть особый способ записи и последующего восстановления изображения предмета, основанный на регистрации интерференционной картины. При освещении фотопластинки (голограммы) пучком света изображение предмета восстанавливается в почти первоначальном виде, так что создается ощущение его реальности.
Для записи предмета на светочувствительной пластинке кроме волны, отраженной от предмета (так называемой предметной волны), используется когерентная с ней волна от источника света (так называемая опорная волна). На фотопластинке фиксируется распределение интенсивности в интерференционной картине, возникающей при наложении предметной и опорной волн. При освещении проявленной фотопластинки происходит дифракция света в фотослое. В результате дифракции восстанавливается изображения предмета.
Практически идея голографии осуществляется с помощью схемы, изображенной на рис. Лазерный пучок делится на две части, причем одна его часть отражается зеркалом на фотопластинку (опорная волна), а вторая попадает на фотопластинку, отразившись от предмета (предметная волна). Опорная и предметная волны, являясь когерентными, при наложении интерферируют. Интерференционная картина фиксируется на фотопластинке, после ее проявления получается голограмма – изображение интерференции.
Для восстановления изображения голограмма помещается в то же самое положение, где она находилась до регистрации. Ее освещают опорным пучком того же лазера (вторая часть лазерного пучка перекрывается диафрагмой). В результате дифракции опорной волны возникает несколько волн. Одна волна дает мнимое изображение, которое точно воспроизводит предмет. Другая волна образует действительное изображение предмета. Действительное изображение псевдоскопично – оно имеет рельеф, обратный рельефу предмета (выпуклые места заменены вогнутыми и наоборот). Третья волна является продолжением падающей с меньшей интенсивностью.
Рассмотрим принцип голографии на простом примере. Пусть на фотопластинку падают две когерентные волны, идущих под углом 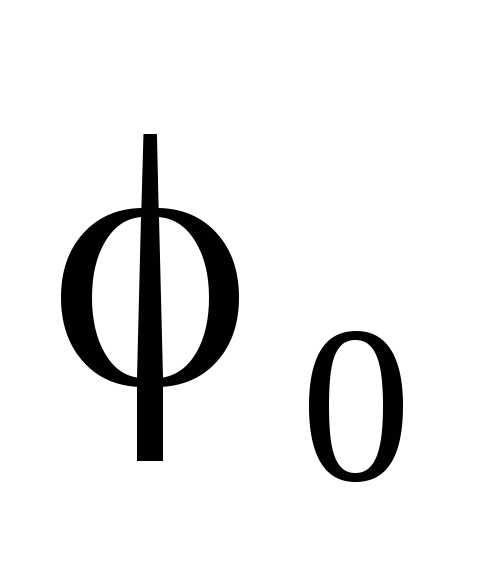 друг к другу. Волна1 является опорной, волна 2 – предметной (предмет в данном случае представляет бесконечно удаленную точку). Для простоты, предположим, что волна 1 падает на пластинку нормально.
друг к другу. Волна1 является опорной, волна 2 – предметной (предмет в данном случае представляет бесконечно удаленную точку). Для простоты, предположим, что волна 1 падает на пластинку нормально.
Вследствие интерференции волн на пластинке образуется (и фиксируется) система прямолинейных полос – максимумов и минимумов интенсивности. Пусть точки a и b соответствуют серединам соседних максимумов. Тогда разность хода соответствующих лучей предметной волны до этих точек равна . Из рис. видно, что разность хода и, следовательно,
. (12)
Направим свет опорной волны на проявленную фотопластинку. Пластинка является дифракционной решеткой, период которой определяется формулой (12). Особенность этой решетки состоит в том, что ее прозрачность изменяется плавно (у обычных решеток она изменялась скачком). Эта особенность приводит к тому, что интенсивность дифракционных максимумов выше 1-го практически равна нулю и результирующая дифракционная картина определяется условием
. (13) Максимумm 0 лежит на продолжении опорного пучка. Максимум m +1 имеет такое же направление, какое имела предметная волна. Кроме того, возникает максимум m 1.
Сходная ситуация возникает и при освещении голограммы, полученной от реального предмета. При этом будет восстановлена световая волна, отраженная предметом (ей отвечает m +1). Кроме нее, возникают еще две волны (отвечающие m 0 и m 1). Последние распространяются в других направлениях и не мешают восприятию мнимого изображения предмета (которое и представляет главный интерес).
Рассмотренный способ дает одноцветные изображения (цвета лазера). Цветное зрение связано с тремя типами светочувствительных элементов сетчатки глаза, реагирующих на красное, зеленое и синее. Зрительное восприятие, поэтому, складывается из трех одноцветных изображений, соответственно красного, зеленого и синего. Это свойство зрения используется в цветной голографии.
Цветная голография основана на записи объемной интерференционной картины. Восстановление изображения происходит при отражении света от голограммы. Схема записи и восстановления цветного изображения приведена на рис. При записи предмет (последовательно или одновременно) освещается излучением трех цветов: красным, зеленым и синим. В толще фотоэмульсии образуется (и фиксируются) три пространственные интерференционные картины. При освещении белым цветом каждая из систем формирует свое одноцветное изображение предмета. В результате, при наложении трех одноцветных, получаются цветное изображение предмета.
studfiles.net